ответ:
tg ∠ spo=sp: op=13: 2=6,5
объяснение:
нарисуем пирамиду, проведем в ней сечение мsk.
мк - средняя линия треугольника cdb, параллельна db и равна ее половине.
диагональ ас квадрата авсd равна диагонали db
ор - четверть этой диагонали и равна 8: 4=2 (из треугольника cdb, в котором высота делится отрезком мк пополам).
sр- высота, биссектриса и медиана треугольного сечения мsk.
небоходимо найти tg ∠ spo, под которым сечение пересекается с плоскостью пирамиды.
нарисуем отдельно треугольник pso.
tg ∠ spo=sp: op=13: 2=6,5
а) sin x - 0,5 = 0
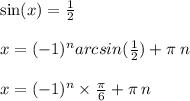
*где n - целое число
Рассмотрим варианты:
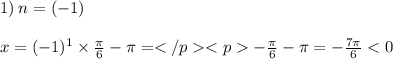
При n=(-1) - х<0 и не принадлежит отрезку [0;2π].
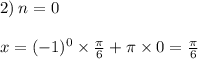
При n=0 - x = π/6 - принадлежит отрезку [0;2π].
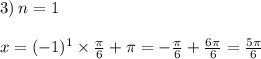
При n=1 - x = (5π/6) - принадлежит отрезку [0;2π].
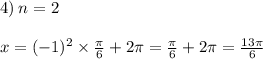
При n=2 - x = (13π/6) - не принадлежит отрезку [0;2π].
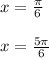
б) tg x - 1 = 0
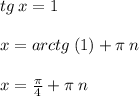
*где n - целое число
Рассмотрим варианты:
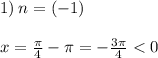
При n=(-1) - х<0 и не принадлежит отрезку [0;2π].
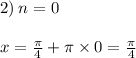
При n=0 - x = π/4 - принадлежит отрезку [0;2π].
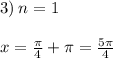
При n=1 - x = (5π/4) - принадлежит отрезку [0;2π].
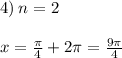
При n=2 - x = (9π/4) - не принадлежит отрезку [0;2π].
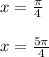
![Найдите корни уравнения, принадлежащие отрезку [0;2пи]: а) sin x - 0,5 = 0; б) tg x - 1 = 0.](/tpl/images/4836/4198/1fe1b.jpg)
а)9х^4 y^12 б)-8a^21 y^21
Объяснение: