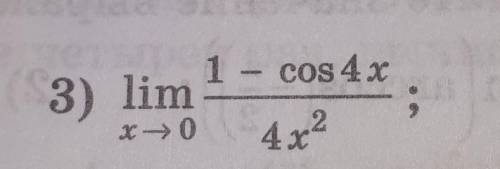

Объяснение:
по следствию из первого замечательного предела
lim (1-cosx)/(x^2/2)=1
x->0
4x^2 умножим и разделим на 2 и 16 получится
4*(16*(x²)/2)*2/16=4[(4x)²/2]/8=[(4x)²/2]/2
=lim (1-cos4x)/4x² =
x->0
=lim (1-cos4x)/[(4x)²/2]/2 =
x->0
=lim 2 (1-cos4x)/[(4x)²/2] = заменим 4x=y
x->0
= 2 lim (1-cosy)/(y^2/2)=2
y->0
нехай перший рухався зі швидкістю х км/год, а другий у км/год. тоді перший пройшов до зустрічі 3х км, а другий 3у км., а разом 3х+3у=27 км за умовою перший прийшов на 1 год 21 хв=1,35 год раніше. тому 27/у-27/х=1,35 складемо систему рівнянь [latex] \left \{ {3x+3y=27} \atop {27/y-27/x=1.35}} \right. [/latex] виразимо в першому рівнянні х через у х=9-у підставимо в друге рівняння 20х-20у=ху . маємо: 180-20у-20у=9у-у² у²-49у+180=0 d=1681 y1=(49+41)/2=45 y2=4 тоді x1=9-45=-36 , що не задов умові і х2=9-4=5 км/год швидкість першого пішохода 5 км/год, а другого 4 км/год