(19, 342), (20, 180), (21, 126), (22, 99), (24, 72), (27, 54) и (36, 36)
Объяснение:
Представим уравнение в другом виде:
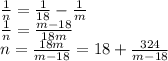
324 можно разложить на простые множители: 2²·3⁴
Значит m-18 должно содержать эти множители. Он может быть равен 1,2,3,4,6,9,18,108 и 324. Соответствующие m для этого: m = 19,20,21,22,24,27,36,126 и 342
При последовательной подстановке этих чисел в уравнении нахождения чисел n, мы получаем: n = 342, 180, 126, 99, 72, 54, 36, 21 и 19. Среди них подходят пары (19, 342), (20, 180), (21, 126), (22, 99), (24, 72), (27, 54) и (36, 36)
ответ: 10 км/час.
Объяснение:
Скорость второго равна х км/час.
Тогда скорость первого равна х+15 км/час.
Время в пути первого 200/(х+15) часов.
Время в пути второго --- 200/х часов.
Разница во времени равна 12 часов.
200/х - 200/(х+15) = 12;
200(x+15) - 200x = 12x(x+15);
200x+3000-200x = 12x²+180x;
12x²+180x -3000=0;
x²+ 15x - 250 = 0;
По теореме Виета:
х1+х2=-15; х1*х2=-250;
x1=10; x2= -25 - не соответствует условию
х=10 км/час -- скорость второго велосипедиста
х+15 = 10+15 = 25 км/час - скорость первого велосипедиста.
Проверим:
200/10 - 200/25 = 20 - 8=12 часов. Всё точно!