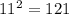. Далее откидываем от вновь получившегося числа ещё одну цифру(то есть стремимся, чтоб число состояло из двух цифр, ибо нужно узнать две последние цифры), получаем 21. 
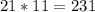. Проделываем ту же операцию ещё несколько раз: 
... Наблюдаем закономерность: который раз мы умножаем получившееся число на 11, такая цифра и будет второй с конца(2011 * 2011 = ...21; ...21 * 2011 = ...31; ...31 * 2011 = ...41; и т.д., притом после накрутки первого десятка вторая цифра онулируется и всё по новой...), а первая с конца всегда единица. Таким образом, 
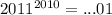, а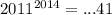 
.
5+10+15+...+290+295+300
Это арифметическая прогрессия.
a1=5; d=5; a(n)=300; n=300/5=60
S(60)=(a1+a60)*60/2=305*30=9150