17
Объяснение:
Попробуем угадать исходную функцию. Рассмотрим слагаемое 21x. Пусть в исходной функции перед x стоял коэффициент C₁. Тогда 2C₁x - (-C₁x) = 3C₁x = 21x ⇒ C₁ = 7. Рассмотрим модули. Заметим, что |-x + a - 5| = |x - a + 5|. Пусть в исходной функции содержалось выражение C₂|x + a - 5| + C₃|x - a + 5|. Тогда для полученных коэффициентов составим систему:
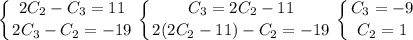
Свободный член не зависит от x, поэтому если в исходной функции было выражение C₄(-8a + 28), то в выражении оно равно 2C₄(-8a + 28) - C₄(-8a + 28) = C₄(-8a + 28) = -8a + 28 ⇒ C₄ = 1.
Значит,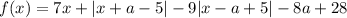 
. График данной функции — некоторая ломаная. Заметим, что характер возрастания и убывания определяет то, как раскроется модуль |x - a + 5|. Даже если другой модуль раскроется с плюсом, то коэффициент перед x при x ≥ a - 5 равен 7 + 1 - 9 = -1 < 0, то есть при x ≥ a - 5 функция убывает. Аналогично если первый модуль раскроется с минусом, при x < a - 5 коэффициент перед x равен 7 - 1 + 9 = 15 > 0, то есть при x < a - 5 функция возрастает. Значит, x = a - 5 — точка максимума функции. Если в ней значение функции неположительно, то и для всех остальных x требуемое неравенство выполняется.
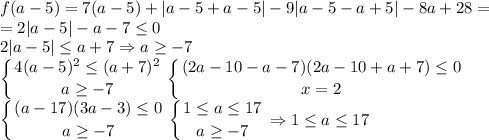
Наибольшее значение параметра — 17.
Дано функцію f(x) = (x^2-8x)/(x+1)
Знаходимо найбільше і найменше значення даної функції на проміжку [-5,-2].
f(-5) = ((-5)^2-8*(-5))/(-5+1) = 65/(-4) = -16,25.
f(-2) = ((-2)^2-8*(-2))/(-2+1) = 20/(-1) = -20.
Визначаємо точки екстремуму даної функції.
Знаходимо первісну:
f'(x) = (2x-8)*(x+1) - 1*(x^2-8x))/((x+1)^2) = (x^2 + 2x - 8)/((x + 1)^2).
Прирівнюємо їі до 0 (достатьно чисельник):
x^2 + 2x - 8 = 0, Д = 4+4*8 = 36, х1 = (-2 - 6)/2 = -4, х2 = (-2 + 6)/2 = 2.
Знаходимо знаки первісної:
х = -5 -4 1 2 3
y' = 0,4375 0 -1,25 0 0,4375 .
У точці х = -4 маємо максимум функції,
f(-4) = ((-4)^2-8*(-4))/(-4+1) = 48/(-3) = -16.
Відповідь:
- найбільше значення даної функції на проміжку [-5,-2] дорівнює -16,
- найменше значення даної функції на проміжку [-5,-2] дорівнює -20,
- максимум функції у точці х = -4,
- мінімум функції у точці х = 2.
1) |3x - 4y -2 | + |x - 5y +3 | = 3х-4у-2+х-5у+3 = 4х-9у+1 при
3x - 4y -2 > 0 и x - 5y +3 > 0
2) |3x - 4y -2 | + |x - 5y +3 | = -3x+4y+2+x-5y+3 = -2x-y+5 при
при 3x - 4y -2 < 0 и x - 5y +3 > 0
3) |3x - 4y -2 | + |x - 5y +3 | = 3х-4у-2-х+5у-3 = 2x+y-5 при
3x - 4y -2 > 0 и x - 5y +3 < 0
4) |3x - 4y -2 | + |x - 5y +3 | = -3х+4у+2-х+5у-3 = -4х+9у-1при
3x - 4y -2 < 0 и x - 5y +3 < 0