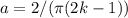 ,
, 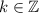 , но для них будет всегда больше одного решения, т.к. даже при самом большом значении a при k=0 и k=1 прямая (ax+1)/2 пересечет график cos(x) в трех точках. А значит, при всех остальных а угол наклона прямой будет еще меньше, и, значит, пересечений с косинусом будет еще больше.
, но для них будет всегда больше одного решения, т.к. даже при самом большом значении a при k=0 и k=1 прямая (ax+1)/2 пересечет график cos(x) в трех точках. А значит, при всех остальных а угол наклона прямой будет еще меньше, и, значит, пересечений с косинусом будет еще больше.
x=0 y=0
Для х>0 y=x²-6x
y=x²-6x=0 x(x-6)=0 x₁=0 x₂∞=6
y`=2x-6=0
x=3
y(3)=3²-3*6=-9=ymin (3;-9)
0-3++∞
убывает возрастает
Для х<0 y=x²+4x
y=x²+4x=0 x(x+4)=0 x₁=0 x₂=-4
y`=2x+4=0
x=-2
y(-2)=(-2)²+4*(-2)=-4=ymin (-2;-4)
-∞--2+0
убывает возрастает
↑ Y
° I °
I
I
° I °
I O X -4 -2o36
° ° I ° °
I ° °
° ° I
° -4 I ° °
I
I ° °
I ° °
-8 I °
m=-8 - одна общая точка.
m∈(-4;-8)∨(0;+∞) - две общие точки.
m∈[-4;0] - три общие точки.