скорее всего 2) 343 на 10
Философия Древней Греции, в своей основе, представляла учение о рациональном осмыслении существования мира. В те времена, никто не сомневался в божественном происхождении всего сущего, но учения о том, как, по какому принципу, создана окружающая действительность, оставили заметный след в науке и культуре Западного мира, ставших основой принципов и методов научного познания вселенной.
Пифагор Самосский - загадочная, но достоверно существовавшая, личность. Являясь религиозным философом - идеалистом, он создал тайное учение, записи о котором вести запрещалось, поэтому до нас не дошло ни одного трактата самого Пифагора. О достижениях Пифагора и Пифагорейской школы, известно из свидетельств античных авторов, появившихся после 3 века до н. э.
Известно, что Пифагор родился, приблизительно, в 750 г. до н. э . в Самосе (или Сидоне). В 18 лет он покинул Грецию и, прожив в Египте 22 года, постиг тайные учения египетских мудрецов и магов, потом, в плену в Вавилоне, в течение 12-и лет, продолжал общение с членами магических тайных обществ.
В 56 лет Пифагор вернулся на родину уже состоявшимся философом, - кстати, Пифагор, первым из греческих мудрецов, назвал себя философом - любителем мудрости, - и создал свою школу тайного учения.
Девизом Пифагорейской школы можно назвать изречение "Цифры правят миром". Учение Пифагора делится на две части : научный подход к познанию мира и религиозно - мистические постулаты образа жизни. Второй частью предписывались нравственное и физическое очищение, как средство достижения идеального существования, в ней содержались сведения о круговороте человеческой жизни, морально - этические общечеловеческие законы.
Первая часть, тайное учение, была уделом посвященных. В ней содержались принципы построения вселенной и всего сущего. Пифагор считал, что миром правят числа, и, что познание мира - это познание чисел, им управляющих.
Пифагорейская школа выдвинула гипотезу о количественной закономерности развития мира мира, что стало основой для развития точных наук.
В Древней Греции, синонимом красоты была гармония. А философия включала в себя не только мудрые размышления о сущем, но и науку, искусства и спорт. Пифагорейцы искали математические основы гармонии, и открыли числовые отношения (пропорции) во всех сферах человеческой деятельности. Платон писал: "Математика выявляет порядок, симметрию и определённость, а это – важнейшие виды прекрасного."
Благодаря поиску гармонии и открытию пропорций, Пифагором была открыта математическая закономерность музыкального звучания - Теория музыки. Это были бесценные опыты доказательства связи физического явления (звук) с математическими законами.
Пифагор использовал три средние величины (а, может, и был их первооткрывателем): среднее арифметическое, геометрическое и гармоническое.
Он, первым, доказал теорему " В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов", носящую его имя.
Пифагор занимался изучением четных и нечетных чисел, применяя, впервые, дедуктивный метод исследования. (от частного - к общему). Одним из первых объектов изучения, в современной Теории чисел, была теория четных и нечетных чисел.
Также, Пифагор доказал теорему о сумме внутренних углов треугольника, изобрел (по некоторым источникам), таблицу умножения в современном виде, нашел геометрический решения квадратных уравнений, разработал правила решения задач.
Поскольку, в Пифагорейской школе, записи были под запретом, и знания передавались от учителя к ученикам устно, то, среди исследователей, есть разногласия по поводу авторства Пифагора в тех или иных исследованиях, проводившихся в рамках его школы. Приписываемые Пифагору открытия, вполне могут быть открытиями его учеников. Кроме того, существует мнение, что все, что было открыто, доказано и разработано школой, являлось интеллектуальной собственностью Пифагора. Несмотря на подобные разногласия. несомненно то, что школа была основана на научных и философских изысканиях Пифагора, в ее основу легли его теории существования вселенной и, все открытия школы имели заданное направление, поэтому, без сомнения, их можно считать открытиями самого великого философа.
Заметим ,что наименьшие значения функций:
2^(x-3) +4>4
5*|tg(x)|+3*|ctg(x)|>=2√15 (из соображений полного квадрата и положительности каждого из членов |tg(x)|*|ctg(x)|=1)
Рассмотрим случай когда : a<-2√15
В этом случае числитель будет отрицателен при любом x:
a-(2^(x-3) +4)<0
Знаменатель же ,будет положителен не всегда, тк при каком нибудь x обязательно найдется значение 5*|tg(x)|+3*|ctg(x)|>a ,тк оно имеет область значений от 2√15 до бесконечности) . То есть в зависимости от x, может быть как и положителен так и отрицателен. Вывод: при a<-2√15 будут существовать решения неравенства.
Рассмотрим случай когда: a>4
Тут ситуация иная:
Знаменатель тут всегда положителен,а вот числитель не всегда отрицателен,то есть решения так же будут существовать .
Наконец рассмотрим случай когда:
-2√15<=a<=4
В этом случае числитель всегда отрицателен (при любом x), а знаменатель же наоборот будет неотрицателен. Таким образом только на этом интервале неравенство не будет иметь решения не для какого x. Тк отношение числителя и знаменателя всегда будет отрицательным. P.S Не у кого тут нет вопросов почему строгое неравенство для -2√15(знаменателю быть равным нулю не запрещается,тк наша цель отсутствие решений). Почему же строгое и для 4, а дело все в том ,что: 2^(x-3) +4≠4 , а только стремится к нему при стремлении x к бесконечности,поэтому опасаться за равенство нулю числителя не стоит.
Таким образом
ответ: a∈[-2√15;4]
0.7*0.07*0.000007=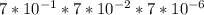 =343*10- 9
=343*10- 9