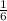 ( т.к. надо разделить благоприятные исходы на кол-во всех событий. 2) Всего событий- 6 ( по той же причине , что и в первой) Благоприятных исходов- 3 (т.к. менее 4 очков должно выпасть, а это, либо 1 либо 2 либо 3) Р(В)=
( т.к. надо разделить благоприятные исходы на кол-во всех событий. 2) Всего событий- 6 ( по той же причине , что и в первой) Благоприятных исходов- 3 (т.к. менее 4 очков должно выпасть, а это, либо 1 либо 2 либо 3) Р(В)=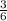 , а это равно
, а это равно 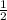 ( или по другому 0,5)
( или по другому 0,5)
0х=13
х - не будет иметь решений