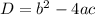
пусть 3x=t
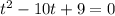
D=100-4*9=64
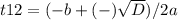
t1=9
3x=9
x=2
и
t2=1
3x=1
x=0
7–10. Два уравнения называют равносильными, если они имеют одинаковые корни или если оба уравнения не имеют корней. Решаем уравнения, находим корни уравнения и сравниваем ответы.
7. 1)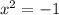 
число в корне не может равняться отрицательному числу, корней уравнения нет.
2) 
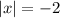
число в модуле не может равняться отрицательному числу, корней уравнения нет.
=> уравнения равносильные.
8. 1)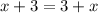 
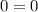
корней уравнения нет.
2) 
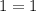
корней уравнения нет.
=> уравнения равносильные.
9. 1) 
ОДЗ: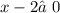 
, 
;
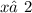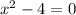
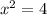
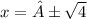
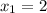(не удовлетворяет ОДЗ), 
ответ: 
2)
,
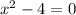
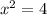
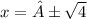
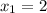ответ: ; 
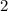
=> уравнения не равносильные.
10. 1)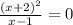 
ОДЗ: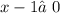 
, 
;
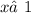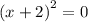
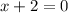
ответ:
2)
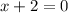
ответ:
=> уравнения равносильные.
12–16. Необходимо найти сумму корней уравнения. Решаем уравнение, находим корни уравнения, складываем их. Если уравнение имеет один корень, то суммой (ответом) будет значение корня уравнения.
12. 
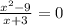
ОДЗ: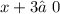 
, 
;
, 
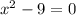
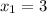(не удовлетворяет ОДЗ)
ответ: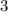 
13. 
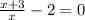
ОДЗ: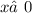 
;
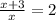
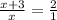
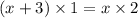
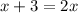
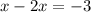
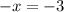
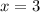
ответ: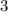
14. 
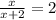
ОДЗ: 
, 
;
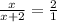
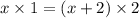
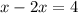
ответ: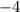 
15. 
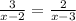
ОДЗ: , ,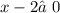 
, 
;
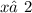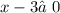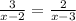
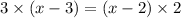
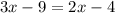
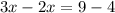
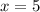
ответ: 
16. 
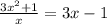
ОДЗ: ;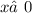
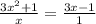
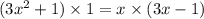
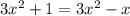
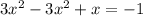
ответ: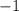 
7
Объяснение:
число 7
сумма цифр квадрата предыдущего числа, увеличенного на 1
тут написано увеличенного
предыдущего числа увеличенного на 1 сумма цифр квадрата
тут не написано "сумма цифр квадрата предыдущего числа, увеличенное на 1"
поэтому сначала прибавляем к предыдущему числу 1, находим квадрат и находим сумму цифр
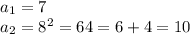
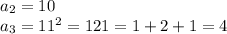
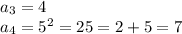
и теперь числа повторяются
каждые 3 раза числа заканчиваются на 4
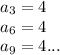
поделим 2011 на 3
оно не делится так как сумма цифр 2+1+1=4 не делится на 3
изменим число 2011 на число поменьше
например 2010 и оно уже делится на 3
поделим
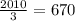то есть оно реально делится, а это значит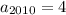 
по логике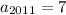 
так как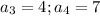 
По теореме Виета:
Если не знаете теорему Виета то можно заменить: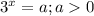
, тогда получите квадратное уравнение и те же ответы