
Данная функция - квадратичная (функция, уравнение которой включает в себя переменную 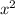 ). Стандартный вид функции:
). Стандартный вид функции: 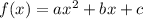 .
.
То есть в нашей функции 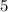 это
это  ,
, 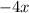 это
это 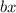 и
и 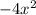 это
это 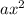 .
.
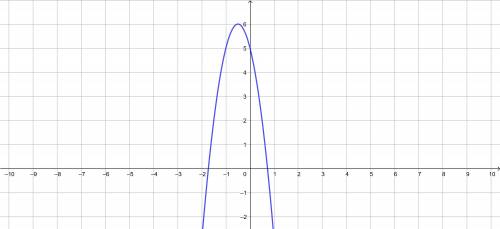
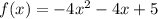 .2. Определим направление параболы.
.2. Определим направление параболы.График квадратичной функции - парабола (геометрическое место точек, равноудалённых от данной прямой). Ветви параболы могут быть направлены вверх и вниз.
Если коэффициент  при переменной
при переменной 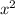 положительный, то ветви параболы направлены вверх. Если же коэффициент отрицательный, то ветви параболы направлены вниз.
положительный, то ветви параболы направлены вверх. Если же коэффициент отрицательный, то ветви параболы направлены вниз.
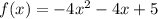 . Здесь
. Здесь 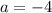 , поэтому ветви параболы направлены вниз.3. Вычислим координату
, поэтому ветви параболы направлены вниз.3. Вычислим координату  вершины параболы.
вершины параболы.Координата  вершины параболы - значение
вершины параболы - значение 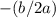 . Если квадратичная функция записана в стандартном виде
. Если квадратичная функция записана в стандартном виде 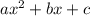 , воспользуемся коэффициентами
, воспользуемся коэффициентами  и
и 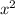 :
:
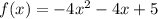 коэффициенты
коэффициенты 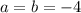 . Т.е. координата
. Т.е. координата  вершины параболы:
вершины параболы: 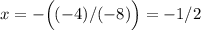 .4. Найдём соответствующее значение
.4. Найдём соответствующее значение 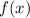 .
.Мы ищем максимум функции, так как ветви параболы направлены вниз. Чтобы найти максимум нужно подставить в исходную функцию 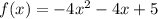 найденное значение
найденное значение  .
.
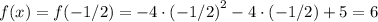 5. Запишем окончательный ответ.
5. Запишем окончательный ответ.Точка максимума функции равна  .
.
1) 24 : 3 = 8 (ябл.) — стало у каждого брата;
1) 8 • 2 = 16 (ябл.) — было у старшего брата до того, как он делился яблоками;
2) 8 : 2 = 4 (ябл.) — по столько дал старший брат младшему и среднему;
3) 8 - 4 = 4 (ябл.) — по столько было у среднего и младшего до того, как делился старший брат;
4) 4 • 2 = 8 (ябл.) — было у среднего брата до того, как он делился яблоками;
1) 4 : 2 = 2 (ябл.) — дал средний брат старшему и младшему;
2) 16 — 2= 14 (ябл.) — было у старшего брата до того, как делился средний;
3) 4 - 2 = 2 (ябл.) — было у младшего брата до того, как делился средний;
4) 2 • 2 = 4 (ябл.) — было у младшего брата изначально;
5) 2 : 2 = 1 (ябл.) — дал младший брат старшему и среднему;
6) 14-1 = 13 (ябл.) — было у старшего изначально;
7) 8 - 1 = 7 (ябл.) — было у среднего брата изначально.
ответ: 4; 7; 13.
РЕШЕНИЕ СМОТРИ НА ФОТОГРАФИИ
Объяснение: