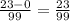
z = x*y
1. Найдем частные производные.
2. Решим систему уравнений.
y = 0
x = 0
Получим:
а) Из первого уравнения выражаем x и подставляем во второе уравнение:
x = 0
y = 0
Откуда y = 0
Данные значения y подставляем в выражение для x. Получаем: x = 0
Количество критических точек равно 1.
M1(0;0)
3. Найдем частные производные второго порядка.
4. Вычислим значение этих частных производных второго порядка в критических точках M(x0;y0).
Вычисляем значения для точки M1(0;0)
AC - B2 = -1 < 0, то глобального экстремума нет.
Вывод: Глобального экстремума нет.
1)Раскрываем по определению модуля и получаем совокупность двух систем:
1-ая система: x<-1, -x-1>=3x+7 => -4x>=8 => x<=-2, получается промежуток (-бесконечности;-2]
2-ая система: x>=-1, x+1>=3x+7 => -2x>=6 => x<=-3, здесь получается, что пусто.
Следовательно, ответ: -2
2)По определению логарифмов, получаем, что 1.9x-1.3>=-1^(2.5) => 1.9x>=0.3 => x>=(3/19)
3)Решение: 5^(7x+3)-1/5>=0 => 5^(7x+3)>=1/5
1/5=5^(-1) => 7x+3>=-1 =>7x>=-4 => x>=-4/7