1)y=8/x+3
Уравнение графика гиперболы
Придаём значения х, получаем значения у:
Таблица
х у
-10 2,2
-8 2
-6 1,7
-4 1
-3 0,3
-2 -1
-1 -5
0 -
1 11
2 7
4 5
8 4
2)у=[2/(х-1)]+1
Придаём значения х, получаем значения у:
Таблица
х у
-10 0,8
-8 0,8
-5 0,7
-3 0,5
-1 0
0 -1
1 -
2 3
4 1,7
6 1,4
8 1,3
3)y= -(x+1)²+4
Уравнение параболы со смещённым центром, ветви параболы направлены вниз.
Координаты вершины параболы (-1; 4)
Точки пересечения с осью Х, нули функции (-3; 0) (1; 0)
Точка пересечения с осью У (0; 3)
Дополнительные точки:
Придаём значения х, получаем значения у:
Таблица
х у
-5 -12
-4 -5
-2 3
2 -5
3 -12
1) у=(1/3)х+2 1/3
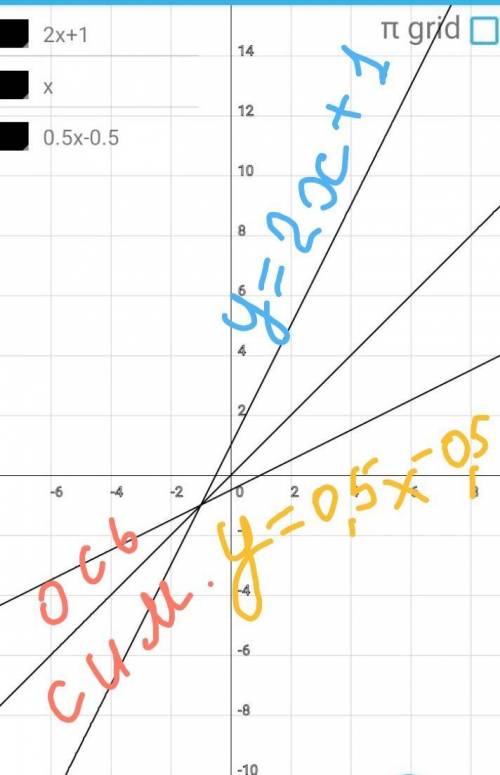
2) у=0,5х-0,5
Объяснение:
1.
у=3х-7
-3х=-у-7
Выразим х через у:
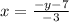
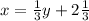
Поменяем местами х и у:
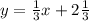
Это уравнение обратной функции.
2.
у=2х+1
Выразим х через у:
-2х=-у+1
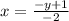
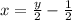
Поменяем местами х и у:
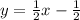
у=0,5х-0,5
Это уравнение обратной функуии.
3.
Известно, что графики прямой и
обратной функций симметричны
относительно биссектрисы 1 коор
динатной четверти.
В одной систеие координат пост
роим графики прямой и обратной
функций. Оба графика - прямые
линии, поэтому достаточно запол
нить таблицу для двух точек.
Таблица для прямой функции:
х 0 2
у -7 -1
Таблица для обратной функции"
х -6 3
у 1/3 1
Оба графика строим в одной ко
ординатной плоскости.
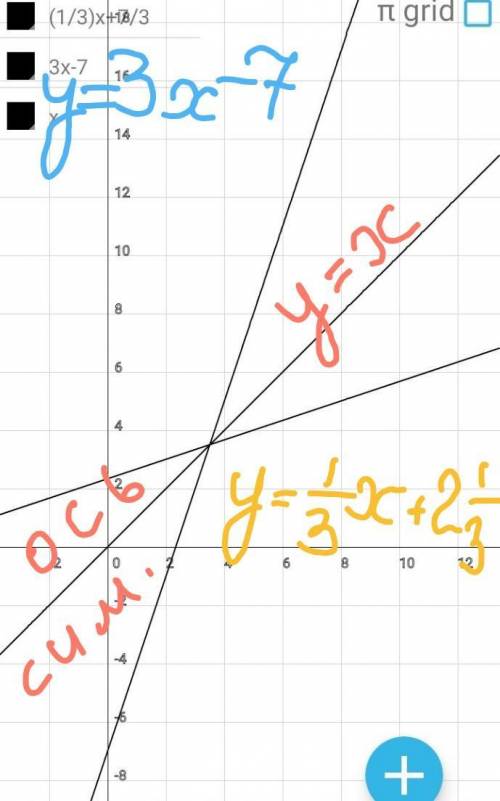
оололо
Объяснение: