а) 3 прямые имеют наибольшее число точек пересечения 3 ,
б) 4 прямые - 6 точек пересечения ,
в) 5 прямых - 10 точек пересечения ,
г) n прямых - \frac{n(n-1)}{2}
2
n(n−1)
точек пересечения .
Решение. Заметим, что наибольшее число точек попарных пересечений получается, если каждая прямая пересекается с каждой и при этом никакие три прямые не пересекаются в одной точке. В этом случае количество точек попарных пересечений равно количеству пар прямых из данного множества n прямых. Как мы знаем, это число равно \frac{n(n-1)}{2}
2
n(n−1)
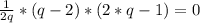
Решение
х кг сена ежедневно выдают одной лошади
у кг сена ежедневно выдают одной лошади
Система из двух уравнений
1) ( 2х+у = 34
2) ( х+2у = 35
умножим второе уравнение системы на ( -2) и сложим с первым, тогда
-3у = -36
у = 12
тогда х+24 =35
х= 11
ответ
11 кг корове
12 кг -лошади