Напишите выражения для нахождения площади поверхности куба, используя формулу

👇

Открыть все ответы

Ответ:

galinaegi2

06.03.2023

На одну четверку должна приходиться одна пятерка. Тогда среднее значение будет 4,5, то на усмотрение педагога получается. Если же число пятерок превышает число четверок, то тут бесспорная "пятерка".

А если на одну тройку приходится две пятерки, то среднее 4,33. Не хватает.

Если на тройку три пятерки, то среднее 4,5, опять же на усмотрение учителя

Если же на тройку приходится четыре пятерки, то среднее 4,6. И тут уж ничего не попишешь, нужно ставить пять в четверти.

Поэтому, чтобы не было сомнений нужно исправлять "тройку" четырьмя "пятерками"

4,4(51 оценок)

Ответ:

gree04

06.03.2023

Решение:

Немного теории. Систему уравнений можно записать в следующем виде:

A·x = b

где A - матрица коэффициентов, x - вектор-столбец переменных, b - вектор-столбец свободных членов.

Умножим эту систему на обратную матрицу коэффициентов A⁻¹ слева. Тогда:

A⁻¹·A·x = A⁻¹·b

x = A⁻¹·b

Таким образом, чтобы решить систему уравнений, нужно найти обратную матрицу коэффициентов и умножить ее на вектор-столбец свободных членов.

1) Обратная матрица

Будем искать обратную матрицу через алгебраические дополнения. Для начала найдем определитель матрицы A :

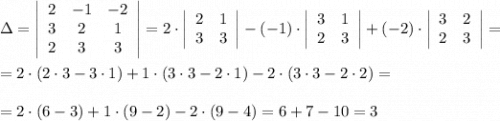
$\Delta =\left|\begin{array}{ccc}2&-1&-2\\3&2&1\\2&3&3\end{array}\right|=2\cdot \left|\begin{array}{cc}2&1\\3&3\end{array}\right|-(-1)\cdot \left|\begin{array}{cc}3&1\\2&3\end{array}\right|+(-2)\cdot \left|\begin{array}{cc}3&2\\2&3\end{array}\right|=\\\\=2\cdot(2\cdot3-3\cdot1)+1\cdot(3\cdot3-2\cdot1)-2\cdot(3\cdot3-2\cdot2)=\\\\=2\cdot(6-3)+1\cdot(9-2)-2\cdot(9-4)=6+7-10=3$

Найдем элементы матрицы алгебраических дополнений:

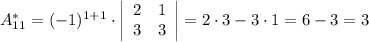
$A_{11}^{*}=(-1)^{1+1}\cdot \left|\begin{array}{cc}2&1\\3&3\\\end{array}\right|=2\cdot3-3\cdot1=6-3=3$

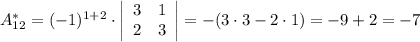
$A_{12}^{*}=(-1)^{1+2}\cdot \left|\begin{array}{cc}3&1\\2&3\\\end{array}\right|=-(3\cdot3-2\cdot1)=-9+2=-7$

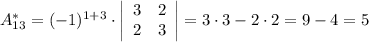
$A_{13}^{*}=(-1)^{1+3}\cdot \left|\begin{array}{cc}3&2\\2&3\\\end{array}\right|=3\cdot3-2\cdot2=9-4=5$

$A_{21}^{*}=(-1)^{2+1}\cdot \left|\begin{array}{cc}-1&-2\\3&3\\\end{array}\right|=-((-1)\cdot3-3\cdot(-2))=3-6=-3$

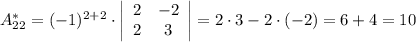
$A_{22}^{*}=(-1)^{2+2}\cdot \left|\begin{array}{cc}2&-2\\2&3\\\end{array}\right|=2\cdot3-2\cdot(-2)=6+4=10$

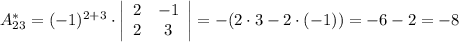
$A_{23}^{*}=(-1)^{2+3}\cdot \left|\begin{array}{cc}2&-1\\2&3\\\end{array}\right|=-(2\cdot3-2\cdot(-1))=-6-2=-8$

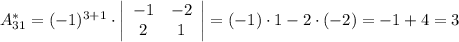
$A_{31}^{*}=(-1)^{3+1}\cdot \left|\begin{array}{cc}-1&-2\\2&1\\\end{array}\right|=(-1)\cdot1-2\cdot(-2)=-1+4=3$

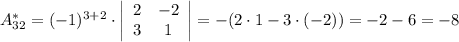
$A_{32}^{*}=(-1)^{3+2}\cdot \left|\begin{array}{cc}2&-2\\3&1\\\end{array}\right|=-(2\cdot1-3\cdot(-2))=-2-6=-8$

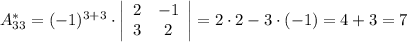
$A_{33}^{*}=(-1)^{3+3}\cdot \left|\begin{array}{cc}2&-1\\3&2\\\end{array}\right|=2\cdot2-3\cdot(-1)=4+3=7$

Тогда:

$A^*=\left(\begin{array}{ccc}3&-7&5\\-3&10&-8\\3&-8&7\end{array}\right)$

Транспонированная матрица алгебраических дополнений:

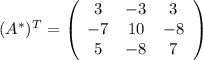
$(A^*)^T=\left(\begin{array}{ccc}3&-3&3\\-7&10&-8\\5&-8&7\end{array}\right)$

Обратная матрица:

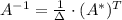
$A^{-1}=\frac{1}{\Delta} \cdot (A^*)^T$

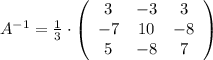
$A^{-1}=\frac{1}{3}\cdot \left(\begin{array}{ccc}3&-3&3\\-7&10&-8\\5&-8&7\end{array}\right)$

2) Вектор-столбец переменных

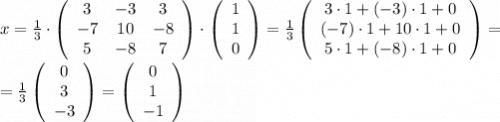
$x=\frac{1}{3}\cdot \left(\begin{array}{ccc}3&-3&3\\-7&10&-8\\5&-8&7\end{array}\right)\cdot\left(\begin{array}{ccc}1\\1\\0\end{array}\right)=\frac{1}{3} \left(\begin{array}{ccc}3\cdot1+(-3)\cdot1+0\\(-7)\cdot1+10\cdot1+0\\5\cdot1+(-8)\cdot1+0\end{array}\right)=\\\\=\frac{1}{3} \left(\begin{array}{ccc}0\\3\\-3\end{array}\right)=\left(\begin{array}{ccc}0\\1\\-1\end{array}\right)$