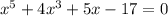и 
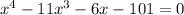, так как -17 и -101 на -7 нацело не делится
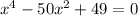корни х=-7, х=7, х=1 и х=-1;
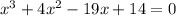его необходимо разложить на множители, т.е. столбиком поделить на х+7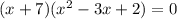
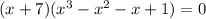
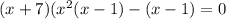
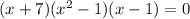
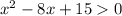
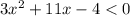, решение между корнями
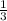, тогда -4<x<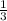
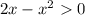
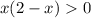
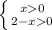
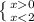решение данной системы является 0<x<2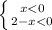
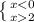эта система решений не имеет, тогда ответ один 0<x<2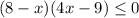
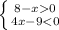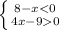
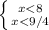и 
и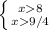 
Линейная функция.