Объяснение:
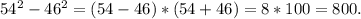
3/7
Объяснение:
x - числитель.
Начальная дробь: x/(x+4), где x - натуральное число.
Система неравенств:
(x+6)/(x+4+4)<(2x)/(x+4); (x+6)/(x+8)<(2x)/(x+4)
(x+8)/(x+4+1)>(3x)/(x+4); (x+8)/(x+5)>(3x)/(x+4)
(x+6)(x+4)<2x(x+8)
x²+4x+6x+24<2x²+16x
2x²+16x-x²-10x-24>0
x²+6x-24>0
Допустим: x²+6x-24=0; D=36+96=132
x₁=(-6-2√33)/2=-3-√33 - этот корень не подходит для уравнения, так как x -
натуральное число.
x₂=(-6+2√33)/2=√33 -3 - этот корень также не подходит для уравнения, так как x -
натуральное число.
При 0≤x<√33 -3: (2+6)/(2+8)<(2·2)/(2+4); 24/30>20/30 - неравенство не
выполняется.
При x>√33 -3: (3+6)/(3+8)<(2·3)/(3+4); 21/28<24/28 - неравенство выполняется.
Следовательно, для данного 1-го неравенства x∈[3; +∞).
(x+8)(x+4)>(3x)(x+5)
x²+4x+8x+32>3x²+15x
3x²+15x-x²-12x-32<0
2x²+3x-32<0
Допустим: 2x²+3x-32=0; D=9+256=265
x₁=(-3-√265)/4 - этот корень не подходит для уравнения, так как x - натуральное
число.
x₂=(√265 -3)/4 - этот корень также не подходит для уравнения, так как x -
натуральное число.
При x>(√256 -3)/4: (4+8)/(4+5)>(3·4)/(4+4); 8/6<9/6 - неравенство не выполняется.
Отсюда следует, что x=3 - это числитель.
Знаменатель: 3+4=7.
Дробь: 3/7.
Пусть х км/ч - скорость из А в В; 252/х ч - время в пути, тогда
(х + 22) км/ч - скорость из В в А; 252/(х+22) ч - время в пути
33 мин = (33 : 60) ч = 0,55 ч - время остановки
Уравнение:
252/х - 252/(х+22) = 0,55
252 · (х + 22) - 252 · х = 0,55 · х · (х + 22)
252х + 5544 - 252х = 0,55х² + 12,1х
0,55х² + 12,1х - 5544 = 0
Разделим обе части уравнения на 0,55
х² + 22х - 10080 = 0
D = b² - 4ac = 22² - 4 · 1 · (-10080) = 484 + 40320 = 40804
√D = √40804 = 202
х₁ = (-22-202)/(2·1) = (-224)/2 = -112 (не подходит, т.к. < 0)
х₂ = (-22+202)/(2·1) = 180/2 = 90
ответ: 90 км/ч.
Проверка:
252/90 - 252/(90+22) = 0,55
252 : 90 - 252 : 112 = 0,55
2,8 - 2,25 = 0,55
0,55 ч = (0,55 · 60) мин = 33 мин - время остановки
800
Объяснение:
Вычисли применяя формулу сокращенного умножения 54^2-46^2
применим формулу a² -b²=(a-b)(a+b)
(54-46)(54+46)=8·100=800