Пусть одна сторона прямоугольника a, другая b.
Так как прямоугольники , полученные у Коли и Миши после разрезания имеют равные периметры , значит прямоугольники равны
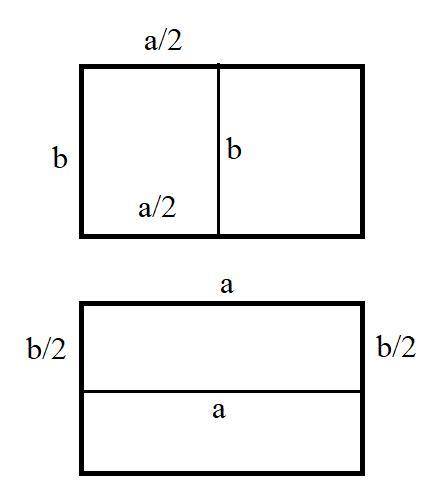
Пусть Коля разрезал сторону а пополам, а Миша сторону b ( cм. рис.)
Тогда периметр прямоугольника у Коли:
Р₁=(a/2)+b+(a/2)+b=a+2b
a+2b=17
Р₂=a+(b/2)+b+(b/2)=2a+b
2a+b=22
Решаем систему уравнений:
{a+2b=17 ⇒ a=17-2b
{2a+b=22
{ a=17-2b
{2·(17-2b)+b=22 ⇒ 34-4b+b=22 ⇒ 34-22=4b-b
3b=12
b=4
2a=22-b
2a=22-4
2a=18
a=9
О т в е т. P=2a+2b=2(a+b)=2(9+4)=26
Объяснение:
№1
А) (2х+1)²= 4х²+4х+1
Б) (3а-с)²= 9а²–6ас+с²
В) (а+6)(а-6)= а²–36
Г) (3х-4у) (3х+4у)= 9х²–16у²
№2
А) у²-¼= (у–½)(у+½)
Б) х²+10х+25= (х+5)²
№3
(2х-у)²-4х(х-у)= 4х²–4ху+у²–4х²+4ху= у²
при у= -⅔
(–⅔)²=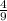
ответ: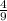
№4
А) 3(2а-b) (2a+b)= 3(4a²–b²)= 12a²–3b²
Б (х⁴+у³)² = (x^8)+2x⁴y³+(y^6)
В) (а+3b)²-(a-3b)²=(a+3b+a–3b)(a+3b–(a–3b))= a²(a+3b–a+3b)= a²*6b= 6a²b
№5
А) (2а-5)²-(2а-3) (2а+3)=0
(4a²–20a+25)–(4a²–9)=0
4a²–20a+25–4a²+9=0
–20a+34=0
20a=34
a=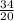
a= 1,7
Б) 9с²-25=0
(3c–5)(3c+5)=0
совокупность:
3с–5=0
3с+5=0
совокупность:
3с=5
3с=–5
совокупность:
с=
с=
совокупность:
с=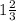
с=