
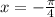
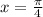
x1=1/4
x2=1/2
Объяснение:
5*√(x^2020) +4*|x| = 5*√( (1-3x)^2020) + 4*|1-3x|
Рассмотрим функцию
f(t) = 5*√(t^2020) +4*|t|
Наше уравнение можно записать в виде :
f(x) = f(1-3x)
Очевидно, что при t >=0 функция f(t) монотонно возрастает при возрастании аргумента t .
Так же очевидно , что функция четная
f(-t) = 5*√((-t)^2020) +4*|-t| = 5*√(t^2020) +4*|t| = f(t) , то есть функция симметрична оси y , причем f(0)=0
Откуда очевидно , что если аргументы t1 и t2 не равны по модулю
|t1|≠|t2| , то и f(t1)≠f(t2) иначе это противоречило бы монотонному возрастанию функции на t>=0 или четности функции.
То есть f(t1) = f(t2) тогда и только тогда , когда аргументы t1 и t2 равны или противоположны .
Иначе говоря |t1|=|t2|
Таким образом из уравнения
f(x) = f(1-3x)
Следует уравнение
|x|=|1-3x|
1) x= 1-3x
4x=1
x1=1/4
2) -x= 1-3*x
2x=1
x2=1/2
Объяснение:
пусть одно число =х, а другое=у, зная итоговый результат составим систему уравнений:
х-у=10
х×у=119
х=10+у
х×у=119
Подставим значение х во второе уравнение: х×у=119
(10+у)у=119
10у+у²=119
у²+10у–119=0
у²+10у-119=0
D=100-4×(-119)=100+476=576
x1= (–10-24)/2= –34/2= –17
x2= (-10+24)=14/2=7
Теперь подставим каждое значение х в первое уравнение: х=10+у
у1=10-17= –7
у2= 10+7=17
Итоги: х1; у1= (–17; -7);. х2; у2=(7; 17)
Проверим найденные данные, подставив их в уравнения: х-у=10; х×у=119
1) -17-(-7)= -17+7= -10;. Первое значение х и у нам не подходит поскольку получается отрицательное число, а нам нужно положительное.
Теперь подставим в уравнения второе значение х и у:
17-7=10;. 17×7=119.
Значения вторые подходят идеально, поэтому:
1-е число =17; 2-е число =7
2
Объяснение:
////////////