/- дробь
1 .
(a**2-ax)/(a**2x-ax**2)
Вынесем за скобки общений множитель и получим
a(a-x)/ax(a-x)
Сократим (a-x) и a
Получаем 1/x
2. (mn**4-cn**4)/(cn**3-mn**3)
Вынесем за скобки общий множитель
n**3(mn-cn)/n**3(c-m)
Сократим на n**3
(mn-cn)/c-m
Вынесем за скобки общий множитель
n(m-c)/(c-m)
Чтобы было одно и тоже сделаем так
n(-(c-m))/(c-m)
Сократим и получим
n* (-1) = -n
3. (4p**2-16p**3)/(12**2-3p)
Вынесем общий множитель
p(4p-16p**2)/p(12p-3)
Сократим
(4p-16p**2)/p(12-3)
Вынесем общий множитель
-4p(-1+4p)/3(4p-1)
Сократим
-4p/3
4) -(x-4)*(x+10)
5) 2(x-1)(x+0.5)
Объяснение:
4)
Первое, что я бы сделал, это избавился от дробных коэффициентов, для этого надо каждый член трёхчлена домножить на 8 и приравнять само выражение 0:
-
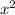-6x +40=0
Находим дискриминант D: 36+160=196.
Так как D > 0, значит у нас будет два x:
x1=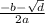
= 
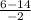= 4
x2=
= 
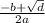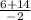=-10
Квадратное уравнение разлагается на множители по формуле: a*(x-x1)(x-x2) - обратите внимание, если х1 и х2 это числовые значения, то X так и записывается X. Таким образом данное уравнение разлагается следующим образом:
ответ: -(x-4)*(x+10)
5) Действуем аналогично, только на этот раз домножаем на 4, чтобы избавится от всех дробей и получаем выражение: 2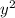
- y -1.
Приравниваем к 0 и решаем квадратное уравнение:
D=1+8=9
D>0, значит есть x1 и x2:
x1,2=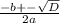
= 
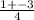= 1 ; -0.5.
Таким образом после разложения на множители получаем:
ответ: 2(x-1)(x+0.5).