и 
Объяснение:
Первый модуль обращается в ноль при x=-2, второй - при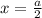 
.
Пусть сначала
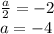
Тогда уравнение принимает вид 
и, очевидно, не имеет решений.
Пусть теперь
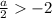
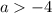
Если 
, то оба модуля раскрываются с плюсом и уравнение принимает вид:
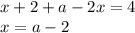
Полученный x будет корнем уравнения, если он принадлежит рассматриваемому отрезку, то есть если 
удовлетворяет системе неравенств
Решение системы: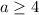 
Если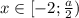 
, то уравнение принимает вид
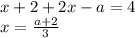
Полученный x будет корнем уравнения, если удовлетворяет системе:
Решение системы: 
Пусть, наконец,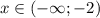 
. Тогда уравнение принимает вид
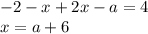
Полученный x будет корнем уравнения, если удовлетворяет системе:
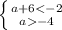
Эта система не имеет решений.
Теперь пусть 
, то есть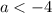 
.
Если 
, то
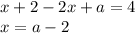
Система:
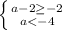
Нет решений.
Если 
, то
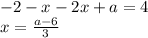
Система:
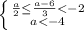
Решение системы: 
И наконец, если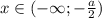 
, то
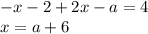
Система:
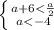
Решение: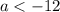 
Из вышесказанного очевидно, что
При 
- два решения
При - одно решение
При 
- нет решений
При 
- нет решений
При - одно решение
При 
- два решения
Таким образом, уравнение имеет одно решение при и
1) ac2-ad+c3-cd-bc2+bd= = (ac2 – ad) + (c3 –
bc2) + (bd – cd) = a·(c2 – d) + c2·(c – b) + d·(b – c) = a·(c2 – d) +
c2·(c – b) – d·(c – b) = a·(c2 – d) + c2·(c – b) – d·(c – b) = a·(c2 –
d) + (c – b)·(c2 – d) = (c2 – d)·(a + c – b)
2) mx2+my2-nx2-ny2+n-m= x2 ( m - n ) + y2 ( m - n ) - ( m - n ) = ( m-n ) (x2 + y2 - 1 )
3) am2+cm2-an+an2-cn+cn2= m2 (a + c ) + n2 ( a + c ) - n ( a + c ) = ( a+ c) ( m2 + n2 - n)
4) xy2-ny2-mx+mn+m2x-m2n= y2 ( x - n ) + m2 ( x - n) - m ( x - n ) = ( x-n) ( y2 + m2 - m )
5) a2b+a+ab2+b+2ab+2=ab ( a + b + 2 ) + ( a+ b+ 2 ) = 2 ( a+ b + 2 )
6) x2-xy+x-xy2+y3-y2= x ( x – y + 1) – y 2 ( x – y + 1)=( x – y + 1)( x – y 2 ).