12см и 8 см
Объяснение:
пусть длина прямоугольника х(см) больше ширины у(см) на 4 см по условию, тогда х = у + 4 (1)
При увеличении меньшей стороны в 2 раза получили 2у, а большую оставили без изменений х. Периметр нового прямоугольника рассчитывается по формуле: Р = 2(a+b), где a и b стороны прямоугольника. Получаем 2(х + 2у) = 56 (2)
Составим систему уравнений из (1) и (2).
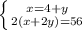 подставляем во второе уравнение вместо х ⇒4+у
подставляем во второе уравнение вместо х ⇒4+у
2(4 + у +2у) = 56 ⇒ 2(4 + 3у) = 56 делим обе части уравнения на 2 ⇒
4 +3у = 28 ⇒ 3у = 28 - 4 ⇒ 3у = 24 ⇒ у = 24 : 3 ⇒ у = 8 (см) ширина.

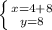
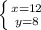
x = 12(см) длина.
область определения функции это множество всех значений, которые может принимать еее аргумент х
D(f)
у дробно рациональных все числа, кроме когда знаменатель = 0
1.3
y = x² + 1/x
x ≠ 0
D(f) = (-∞, 0) U (0, +∞)
y = x - 3/(x + 2)
x ≠ -2
D(f) = (-∞, -2) U (-2, +∞)
y = 5/x + 7/(x + 2)
x ≠ 0 x ≠ -2
D(f) = (-∞, -2) U (-2,0) U (0, +∞)
y = x/(2x - 3) + x²
2x - 3≠ 0 x ≠ 3/2
D(f) = (-∞, 3/2) U (3/2, +∞)
1,4
y = 1/(x² + 2x)
x² + 2x ≠ 0
(x+2)x ≠0
x ≠ 0 x ≠ -2
D(f) = (-∞, -2) U (-2,0) U (0, +∞)
y = 1/(7 - x²)
7 - x² ≠ 0
x ≠ ± √7
D(f) = (-∞, -√7) U U (-√7, √7) U (√7, +∞)
e^(-x)(x+1)dx-((3y/y^2)-4)dy
e^(-x)(x+1)dx=((3y/y^2)-4)dy
Это дифференциальное уравнение первого порядка с разделяющими переменными
Интегрируем почленно это уравнение
∫e^(-x)(x+1)dx=∫((3y/y^2)-4)dy
∫x*e^(-x)dx+∫e^(-x)dx=∫dy/y -4∫dy
1) ∫x*e^(-x)dx
интегрируем по частям
u=x du=dx
e^(-x)dx=dv v=-e^(-x)
тогда интеграл равен
∫x*e^(-x)dx=-x*e^(-x)-∫-e^(-x)dx =-x*e^(-x)-e^(-x)+c1
2) ∫e^(-x)dx=-e^(-x)+c2
3) ∫dy/y=-3/y +c3
4) 4∫dy=4y+c4
или в целом
-x*e^(-x)-e^(-x)+c1-e^(-x)+c2=-3/y +c3+4y+c4
-x*e^(-x)-2e^(-x)+3/y-4y=c- общее решение