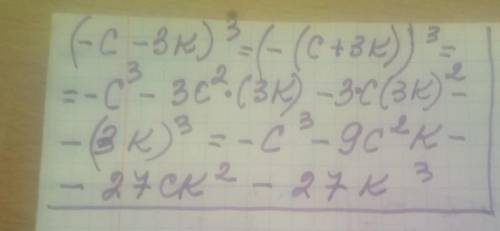
Нужно поднести к кубу. Кто знает, как решить?

Question

Алгебра: Нужно поднести к кубу. Кто знает, как решить?​

maklakovatattu · Accepted Answer

Пусть меньшая сторона — х метров, тогда большая — х+1 метров. Зная площадь площадки, составим и решим мат. модель:

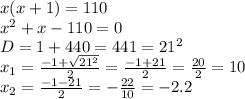
$x(x+1)=110\\x^2+x-110=0\\D = 1+440 = 441 = 21^2\\x_1 =\frac{-1+\sqrt{21^2}}{2} = \frac{-1+21}{2} = \frac{20}{2} =10\\x_2=\frac{-1-21}{2} =-\frac{22}{10} =-2.2$

Отрицательный корень отбрасывает, т.к. длина не может быть отрицательной.

Следовательно, меньшая сторона — х = 10 метров;

большая — х+1 = 10+1 = 11 метров.

Для определения кол-ва упаковок материала для бордюра, вычислим периметр площадки:

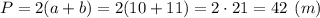
$P= 2(a+b) = 2(10+11) = 2\cdot 21 = 42 \:\: (m)$

Необходимое количество упаковок равно:

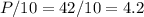
P/10 = 42/10 = 4.2

округляем с избытком до целого числа:

4.2 = 5

Меньшая сторона детской площадки равна: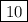 $\boxed {10}$ м.Большая сторона детской площадки равна: $\boxed {11}$ м.Необходимое количество упаковок равно: $\boxed {5}$ .

Нужно поднести к кубу. Кто знает, как решить?​

MOGZ ответил