Задание 1. В некоторых настольных играх нужно бросать кубики, чтобы сделать ход. Сумма очков, выпавших на кубиках, определяет, на какое количество клеток вы продвинетесь. Исследуйте эту случайную величину ("сумма выпавших очков при броске двух кубиков"):
задайте распределение этой случайной величины с таблицы; ( )
найдите математическое ожидание этой случайной величины. ( )
Задание 2 ( ).
Какое из событий более вероятно: "выпадение ровно 3 орлов при 5 бросках монеты" или "выпадение ровно 5 орлов при 7 бросках монеты"?
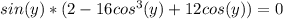
ответ: 1) M[X]=7; 2) более вероятно выпадение 3 орлов при 5 бросаниях монеты.
Объяснение:
1) Случайная величина X - число очков при бросаниях двух кубиков - может принимать значения от 2 до 12.
Событие А2 - выпало 2 очка - может реализоваться только одним :
- на 1 кубике выпало 1 очко и на 2 - тоже 1 очко.
Событие А3 - выпало 3 очка - может реализоваться следующими двумя :
1 и 2 или 2 и 1
Событие А4 - выпало 4 очка:
1 и 3 или 2 и 2 или 3 и 1 - всего .
Событие А5 - выпало 5 очков:
1 и 4 или 2 и 3 или 3 и 2 или 3 и 1 - всего .
Событие А6 - выпало 6 очков:
1 и 5 или 2 и 4 или 3 и 3 или 4 и 2 или 5 и 1 - всего .
Событие А7 - выпало 7 очков:
1 и 6 или 2 и 5 или 3 и 4 или 4 и 3 или 5 и 2 или 6 и 1 - всего .
Событие А8 - выпало 8 очков:
2 и 6 или 3 и 5 или 4 и 4 или 5 и 3 или 6 и 2 - всего .
Событие А9 - выпало 9 очков:
3 и 6 или 4 и 5 или 5 и 4 или 6 и 3 - всего .
Событие А10 - выпало 10 очков:
4 и 6 или 5 и 5 или 6 и 4 - всего .
Событие А11 - выпало 11 очков:
5 и 6 или 6 и 5 - всего .
Событие А12 - выпало 12 очков:
6 и .
Найдём вероятности этих событий. Так как вероятности всех одинаковы и равны 1/6*1/6=1/36, а сами являются несовместными событиями, то:
p(A2)=p(A12)=1*1/36=1/36; p(A3)=p(A11)=2*1/36=2/36; p(A4)=p(A10)=3*1/36=3/36; p(A5)=p(A9)=4*1/36=4/36; p(A6)=p(A8)=5*1/36=5/36; p(A7)=6*1/36=6/36.
Проверка: так как события А2...А12 несовместны и притом образуют полную группу, то p(A2)+p(A3)+...+p(A12)=1. Действительно, 1/36+2/36+3/36+4/36+5/36+6/36+5/36+4/36+3/36+2/36+1/36=36/36=1 - значит, вероятности найдены верно.
Составляем таблицу распределения случайной величины X:
xi 2 3 4 5 6 7 8 9 10 11 12
pi 1/36 2/36 3/36 4/36 5/36 6/36 5/36 4/36 3/36 2/36 1/36
Математическое ожидание M[X}=∑xi*pi=252/36=7.
2) Число m1, которыми можно получить 3 орла при 5 бросаниях монеты, определяется по формуле m1=C(5,3)=10, где C(n,k) - число сочетаний из n по k. А так как вероятность любого p=1/2*1/2*1/2*1/2*1/2=1/32, то вероятность появления 3 орлов при 5 бросаниях монеты p1=10*p=10/32. Число m2, которыми можно получить 5 орлов при 7 бросаниях монеты, определяется по формуле m2=C(7,5)=21. А так как вероятность любого p2=1/2*1/2*1/2*1/2*1/2*1/2*1/2=1/128, то вероятность появления 5 орлов при 7 бросаниях монеты p2=21*p=21/128. Так как p1>p2, то первое событие более вероятно.