объяснение:
выражение ( а - 6 ) * ( а + 2 ) - ( а + 5 ) * ( а - 7 ) и найдем значение выражения при а = - 6,5.
раскрываем скобки. для этого каждые значения в первой скобке, умножаем на каждое значение во второй скобке, и складываем их в соответствии с их знаками. тогда получаем:
( а - 6 ) * ( а + 2 ) - ( а + 5 ) * ( а - 7 ) = a ^ 2 + 2 * a - 6 * a - 6 * 2 - ( a ^ 2 - 7 * a + 5 * a - 5 * 7 ) = a ^ 2 + 2 * a - 6 * a - 12 - ( a ^ 2 - 7 * a + 5 * a - 35 ) = a ^ 2 - 4 * a - 12 - ( a ^ 2 - 2 * a - 35 ) = a ^ 2 - 4 * a - 12 - a ^ 2 + 2 * a + 35 = - 4 * a - 12 + 2 * a + 35 = - 2 * a + 23 = - 2 * ( - 6.5 ) + 23 = 13 + 23 = 36.
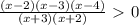

a) 2 sinx cosx - 2√3 cos² x - 4sin x+ 4√3 cos x=0;
(2 sinx cosx- 4sin x)- (2√3 cos² x-4√3 cos x)=0;
2sinx(cos x -2)-2√3 cosx(cosx-2)=0;
(cos x -2)(2 sinx-2√3 cosx)=0;
cos x -2=0; 2 sinx-2√3 cosx=0; / :cos x
cosx=2; 2tg x -2√3 =0;
корней нет tg x =√3;
x=пи/3+пи n, где n целое
б)пи<= пи/3+пи n <= 5пи/2
пи-пи/3<=пи n<= 5пи/2- пи/3
2пи/3<=пи n<=13пи/6
2/3<=n<=13/6 (прим. 2.17) значит рассматриваем корни при n=1 и n=2
n=1: пи/3 + пи = 4пи/3
n=2: пи/3 + 2пи=7пи/3