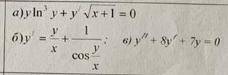
Маленький Принц - це казка лише для дітей, чи для дорослих?
В казці Антуана Де-сент Екзюпері описуються події, які не відбувалися в реальному житті. Тому це казка. Але чи можна вважати, що усі казки для маленьких діточок? Відповідаю - ні. В "Маленькому Принці" розкриваються глибокі моральні теми. Троянда - приклад деяких сучасних жінок, та взагалі людей, які за рахунок оточуючих компенсують свої внутрішні проблеми. Так я це бачу. Але частіше, діти, які читають твір, навіть не помічають цього. Для них - це лише казка. І краще, щоб казка, ще довго залишалася казкою.
Объяснение:
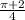
Объяснение:
Сделаем замену переменных:
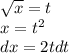
также сразу заменим пределы интегрирования, чтобы не возвращаться к обратной замене:
нижний предел:
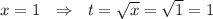
Верхний предел:
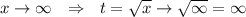
Получаем:
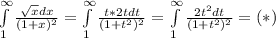
Полученный интеграл не является табличным, поэтому для его решения нужно упростить знаменатель:
Когда в знаменателе стоят выражения 1) 1+x² или 2) 1-x² применяют тригонометрическую или гиперболическую замены.
Для первого случая применяют (на выбор): x=tgt; x=ctgt; x=sht.
Для второго: x=sint; x=cost
В нашем случае применим замену (да, еще одну, такое тоже бывает!)
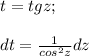
Также заменим пределы интегрирования:
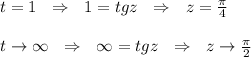
Итого имеем:
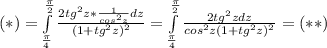
Учитывая, что 1+tg²z=1/cos²z; tg²z=sin²z/cos²z; 2sin²z=1-cos(2z)
Получаем:
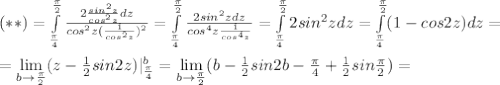
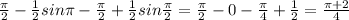
a)
Это ДУ с разделяющимися переменными.
общее решение
2.
однородное ДУ
общее решение
3.
Однородное линейное ДУ
общее решение