ответ: по течению - 20 км/ч, против течения - 16 км/час.
Объяснение: пусть х - собст. скорость лодки, у - скорость течения. За 2 часа по течению лодка пройдет 2(х + у) км, а за 5 часов против течения - 5(х - у) км. Так как вместе она проплыла 120 км, имеем первое уравнение: 2(х+у) + 5(х - у) = 120.
За 7 часов против течения лодка проплыла 7(х - у) км, за 3 часа по течению - 3(х + у) км. Так как 7(х - у) больше чем 3(х + у) на 52, имеем второе уравнение: 7(х - у) - 52 = 3(х + у).
Объединяем оба уравнения в систему (см. ниже). Решая ее, получаем: х = 18 - собст. ск. л., у = 2 - ск. теч. реки. Тогда скорость по течению реки равна 18 + 2 = 20(км/ч), а против течения - 18 - 2 = 16(км/ч).
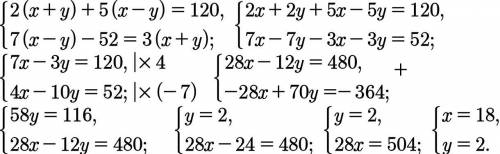
-x^2+4x-6=-(x^2-4x+6)=-((x-2)^2+2)<0
(x^2-4x+6)+|x+5|<=x^2-5x+1
-4x+6+5x-1+|x+5|<=0
x+5+|x+5|<=0
x+5=t
t>=0
2t<=0 t<=0 t=0 x=-5
t<0
0<=0 x<=-5
x=-5