а)

ОДЗ:у-любое число
б)

ОДЗ:у-любое число,кроме у≠9
у-9=0
у=9
в)

ОДЗ:у-любое число, кроме у≠3,у≠ -3
у²-9=0
(у-3)(у+3)=0
у-3=0 или у+3=0
у=3 у= -3
г)

ОДЗ:у-любое число
у²+3=0
у²≠ -3
ответ:уравнение не существует, квадрат числа не может быть отрицательным
д)
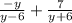
ОДЗ:у-любое число,кроме у≠6,у≠ -6
у-6=0 или у+6=0
у=6 у= -6
е)
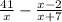
ОДЗ-х-любое число,кроме х≠0,х≠ -7
х=0 или х+7=0
х= -7
II варианта)
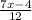
ОДЗ:х-любое число
б)
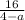
ОДЗ:а-любое число,кроме а≠4
4-а=0
-а= -4
а=4
в)
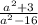
ОДЗ:а-любое число, кроме а≠4,а≠ -4
а²-16=0
(а-4)(а+4)=0
а-4=0 или а+4=0
а=4 а= -4
г)
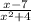
ОДЗ:х-любое число
х²+4=0
х²≠ -4
ответ:уравнение не существует, квадрат числа не может быть отрицательным
д)

ОДЗ:х-любое число,кроме х≠4,х≠ -4
х-4=0 или х+4=0
х=4 х= -4
е)
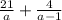
ОДЗ:а-любое число,кроме а≠0,а≠1
а=0 или а-1=0
а=1
ОДЗ-область допустимых значенийкор. 4 ст (x+8) – кор. 4 (x-8) = 2
u^4=x+8 (1)
v^4=x-8 (2)
Тогда
u-v=2
C другой стороны вычтем из (1) (2), получим
u^4 –v^4 = 16
Получаем систему
u-v=2
u^4 –v^4 = 16
Из 1-го уравнения определим u
u = v+2
Подставим во второе уравнение
(v+2)^4-v^4=16
(-v^4-16) + (v^4+8v^3+24v^2+32v+16)=0
8v^3+24v^2+32v=0
v(8v^2+24v+32)=0
Имеем,
v=0
и
8v^2+24v+32=0
v^2+3v+4=0
D=3^2-4-4*1*4=-7 < 0 – нет решений
То есть имеем одно решение v=0, тогда u = v+2=2
u^4=x+8 или x+8=2^4=16, откуда x=8
Відповідь:
Пояснення:
Вероятность попадания р=0.8, промаха q=0.2
2. Не попал не разу Р=q^3=0.2^3=0.008
1. Попал хотяби раз Р= 1-q^3=1-0.008=0.992
3. первый попал, а второй и третий нет. Р=р×q×q=0.8×0.04=0.032