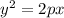ее фокус находится в точке с координатами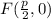 
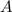находиться в системе уравнения 
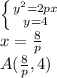Если уравнение касательной равна 
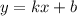с учетом того что она проходит через точку 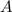получаем 
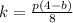, подставляя 
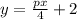
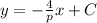он проходит через точку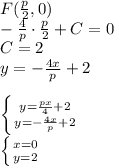 
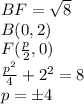
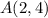
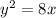
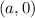центр окружности (так как центр лежит на оси 
) 
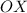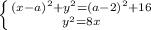
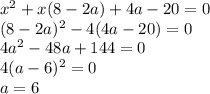
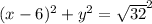
P = 2(a+b), где a и b - стороны прямоугольника
Формула площади прямоугольника:
S = ab, где a и b - стороны прямоугольника
Составляем систему:
2(a+b) = 26,
ab = 42
a+b = 26/2,
ab = 42
a+b = 13,
ab = 42
a = 13-b,
b(13-b) = 42
Работаем с получившимся квадратным уравнением
b(13-b) = 42
-b^2 + 13b - 42 = 0
b^2 - 13b + 42 = 0
По формуле дискриминанта решаем его, получаем корни b1 = 7, b2 = 6
Подставляем значения b для а:
a = 13-b; a1 = 13 - b1 = 13 - 7 = 6, a2 = 13 - b2 = 13 - 6 =7.
Получается, стороны прямоугольника 6 см и 7 см.