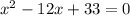Всего 10-значных чисел 9*10^9 Посчитаем, сколько из них чисел, у которых все цифры разные. На 1 месте может стоять любая цифра, кроме 0. 9 вариантов. На 2 месте любая, кроме той, что стоит на 1 месте. 9 вариантов. На 3 месте любая, кроме двух первых. 8 вариантов. И так далее. На 9 месте любая, кроме 8 первых. 2 варианта. На 10 месте стоит одна последняя цифра. 1 вариант. Всего 9*9*8*7*...*2*1 = 9*9! = 3265920 Итак, мы получили: всего 10-значных чисел 9*10^9 = 9000000000 Из них 3265920 чисел, состоящих из всех 10 разных цифр. У остальных 9000000000 - 3265920 = 8996734080 чисел повторяется хотя бы одна цифра.
Всего 10-значных чисел 9*10^9 Посчитаем, сколько из них чисел, у которых все цифры разные. На 1 месте может стоять любая цифра, кроме 0. 9 вариантов. На 2 месте любая, кроме той, что стоит на 1 месте. 9 вариантов. На 3 месте любая, кроме двух первых. 8 вариантов. И так далее. На 9 месте любая, кроме 8 первых. 2 варианта. На 10 месте стоит одна последняя цифра. 1 вариант. Всего 9*9*8*7*...*2*1 = 9*9! = 3265920 Итак, мы получили: всего 10-значных чисел 9*10^9 = 9000000000 Из них 3265920 чисел, состоящих из всех 10 разных цифр. У остальных 9000000000 - 3265920 = 8996734080 чисел повторяется хотя бы одна цифра.
произведение корней равно свободному члены, а их сумма - второму коэффициенту, взятому с противоположным знаком
b=-(x1+x2)=-(6+√3+6-√3)=-(6+6)=-12
c=x1x2=(6+√3)(6-√3)=36-3=33
ответ: