y = 7x - 6sinx + 8
y' = 7 - 6cosx
7 - 6cosx = 0
6cosx = 7
cosx = 7/6, 7/6 больше 1, поэтому корней нет
Раз критических точек нет, то подставляем только границы промежутка:
y(-π/2) = 7*(-π/2) - 6sin(-π/2) + 8 = -7π/2 + 6 + 8 = -7π/2 + 14 = (28-7π)/2
y(0) = 7*0 + sin0 + 8 = 8
Сравним 8 и (28-7π)/2, чтобы определить наибольшее значение:
8 - (28-7π)/2 = (16 - 28 + 7π)/2 = (7π - 12)/2 ≈ (21 - 12)/2 = 9/2 > 0
8 - (28-7π)/2 > 0
8 > (28-7π)/2
ответ: наибольшее значение функции y = 7x - 6sinx + 8 на отрезке [-π/2; 0] равно 8
За умовою, кількість книжок з геометрії відноситься до кількості книжок з алгебри як 2:1. Нехай, книжок з алгебри було x шт., тоді книжок з геометрії - 2x шт. Вірогідність взяти підручник з алгебри дорівнює відношенню кількості підручників з алгебри до кількості всіх підручників, які тільки можна вибрати. Кількість всіх книжок можна порахувати як 2x (книжки з геометрії) + 2 (додаткові книжки з геометрії) + x (книжки з алгебри) + 12 (книжки з інших предметів). Маємо рівняння:
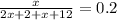
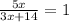
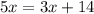
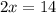
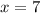
Отже, в нас було 2x = 14 книжок з геометрії і x = 7 книжок з алгебри, всього 14 + 7 + 12 = 33 книжки було спочатку.
Відповідь: 33 книжки.
Объяснение:
10-7/2,8
10-2,5=7,5