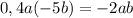
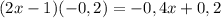
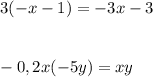
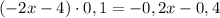
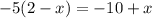
1. 0,4a(-5b) = 0,4 × (-5) × a × b = -2ab
2. (2x - 1)(-0,2) = 2x × (-0,2) -1 × (-0,2) = -0,4x + 0,2
3. 3(-x - 1) = 3 × (-x) + 3 × (-1) = -3x - 3
4. -0,2x(-5y) = -0,2 × (-5) × x × y = 1xy = xy
5. 0,1(-2x - 4) = 0,1 × (-2x) + 0,1 × (-4) = -0,2x - 0,4
6. -5(2 - x) = -5 × 2 - 5 × (-x) = -10 + 5x = 5x - 10
Пусть событие А₁ - "выбран первый кубик (обычный)"
Пусть событие А₂ - "выбран второй кубик (нестандартный)"
Пусть событие В - "выпало сочетание {3; 5} при двукратном бросании кубика"
Поскольку нас интересует вероятность, связанная со вторым кубиком, то распишем вероятность события А₂В двумя :
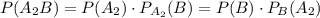
Из этого равенства выразим вероятность того, что брошен был второй кубик, при условии выпадения нужного сочетания:

Знаменатель можно расписать по формуле полной вероятности:
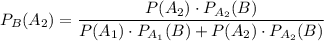
Собственно говоря, записана формула Байеса.
Выбор каждого из кубиков равновероятен:

Вероятность выпадения каждого из имеющихся чисел на первом кубике (от 1 до 6):
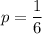
Найдем вероятность выпадения на первом кубике сочетания {3; 5}, учитывая, что этой ситуации соответствует два элементарных исхода (3; 5) и (5; 3):
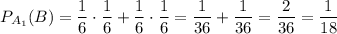
Вероятность выпадения каждого из имеющихся чисел на втором кубике (1, 3, 5):

Найдем вероятность выпадения на втором кубике сочетания {3; 5}:
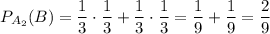
Подставим все значения:
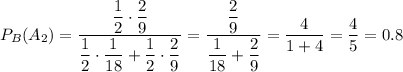
ответ: 0.8
Пусть в викторине участвовали команды А, В, С, D, E, F, причем команды В, С, D проиграли в первых трех раундах команде А.
Тогда, к четвертому раунду в игре остались три команды: А, E, F.
Рассмотрим как они могут располагаться друг относительно друга в зависимости от своей силы (на первом месте запишем сильнейшую команду, на втором - среднюю по силе, на третьем - слабейшую). Это ситуации: AEF, AFE, EAF, EFA, FAE, FEA.
С вероятностью  соперником команды А в четвертом раунде будет команда Е. Тогда, 3 из 6 перечисленных ситуаций окажутся благоприятными. Это ситуации: AEF, AFE, FAE - в них команда А сильнее команды Е.
соперником команды А в четвертом раунде будет команда Е. Тогда, 3 из 6 перечисленных ситуаций окажутся благоприятными. Это ситуации: AEF, AFE, FAE - в них команда А сильнее команды Е.
Значит, вероятность того, что команда А в четвертом раунде будет играть с командой Е и выиграет у нее равна:
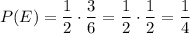
Аналогично, с вероятностью  соперником команды А в четвертом раунде будет команда F. Также, 3 из 6 ситуаций окажутся благоприятными: AEF, AFE, EAF - в них команда А сильнее команды F.
соперником команды А в четвертом раунде будет команда F. Также, 3 из 6 ситуаций окажутся благоприятными: AEF, AFE, EAF - в них команда А сильнее команды F.
Значит, вероятность того, что команда А в четвертом раунде будет играть с командой F и выиграет у нее равна:

Тогда, вероятность того, что команда А выиграет в четвертом раунде равна:
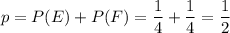
ответ: 1/2