(см. объяснение)
Объяснение:
Теория:
Число делится на 12, если сумма его цифр делится на 3 и запись заканчивается двумя цифрами, образующими число, делящееся без остатка на 4.
Запишем систему:
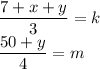
Здесь k и m целые.
Заметим, что:
50+y - четное число, которое делится нацело на 4.Сумма 50+y будет четной, если y четный.Учитывая все вышесказанное, y может принимать значения: 2, 6.
При y=2:
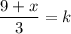
9+x делится на 3, если x равен: 0, 3, 6 или 9.
Значит подходят следующие числа:
2052, 2352, 2652, 2952
При y=6:
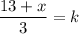
13+x делится на 3, если x равен 2, 5, 8.
Значит подходят следующие числа:
2256, 2556, 2856
Итого ответ:
2052, 2256, 2352, 2556, 2652, 2856, 2952.
Задание выполнено!
№1 (а)
ответ: -\frac{4}{3}" class="latex-formula" id="TexFormula2" src="https://tex.z-dn.net/?f=x%20%3E%20-%5Cfrac%7B4%7D%7B3%7D" title="x > -\frac{4}{3}">
№1 (б)
№2 (а)
-4} \atop {x\leq -2.5}} \right." class="latex-formula" id="TexFormula6" src="https://tex.z-dn.net/?f=%5Cleft%20%5C%7B%20%7B%7Bx%3E-4%7D%20%5Catop%20%7Bx%5Cleq%20-2.5%7D%7D%20%5Cright." title="\left \{ {{x>-4} \atop {x\leq -2.5}} \right.">
№2(б)
\frac{36}{5}" class="latex-formula" id="TexFormula10" src="https://tex.z-dn.net/?f=x%20%3E%20%5Cfrac%7B36%7D%7B5%7D" title="x > \frac{36}{5}">
ответ: \frac{36}{5}" class="latex-formula" id="TexFormula12" src="https://tex.z-dn.net/?f=x%20%3E%20%5Cfrac%7B36%7D%7B5%7D" title="x > \frac{36}{5}">