Действительных корней нет.
Комплексные корни:
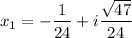
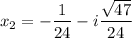
Объяснение:
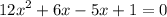
Приводим подобные слагаемые:
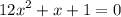
Это обычное квадратное уравнение. Решим через дискриминант.
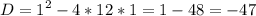
Дискриминант меньше нуля, следовательно действительных корней нет.
Найдем комплексные корни.
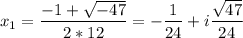
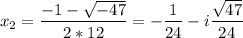
Теория:
Стандартный вид квадратного уравнения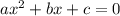 
, 
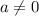
Дискриминант 
Если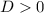 
, то квадратное уравнение имеет два действительных корня.
Если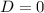 
, то квадратное уравнение имеет один действительных корень.
Если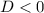 
, то квадратное уравнение не имеет действительных корней, однако комплексные корни существуют.
Комплексное число - число вида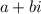 
, где 
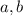- действительные числа, 
- мнимая единица.
Мнимая единица - число, для которого выполняется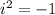 
Нужно чтобы первая скобка не равнялась нулю, и корень не равнялся нулю, но был положительным
х≠ -5
х²+х-6> 0
приравняем к нулю, найдем корни и решим методом интервалов какие значения нам подходят
х²+х-6=0
D=1+24=25
x1= (-1+5)/2=2
x2=(-1-6)/2= -3
методом интервалов получаем:
Хє(-∞;-3)(2;+∞) не забываем что х≠-5
ответ: Выражение имеет смысл :(-∞;-5)(-5;-3)(2;+∞)
Из вышеперечисленных вариантов подходит вариант Г , тоесть при х=4