Алгебра: Докажите что 18³+32³делится на

Докажите что 18³+32³делится на

👇

Увидеть ответ

Ответ:

NatyGranilace

09.04.2020

доказываю.что это делиться на 50 ведь уже ответ есть

4,4(10 оценок)

Открыть все ответы

Ответ:

hjhytu

09.04.2020

По определению, 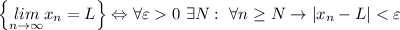$\left\{\underset{n\rightarrow\infty}{lim}x_n=L\right\}\Leftrightarrow\forall\varepsilon 0 \ \exists N: \ \forall n\geq N\rightarrow\left|x_n-L\right|$

Т.к. в обоих случаях нужно обосновать, что L=0, определение преобразуется в утверждение 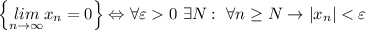$\left\{\underset{n\rightarrow\infty}{lim}x_n=0\right\}\Leftrightarrow\forall\varepsilon 0 \ \exists N: \ \forall n\geq N\rightarrow\left|x_n\right|$

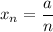
2) $x_n=\dfrac{a}{n}$

|x_n|

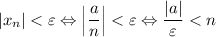
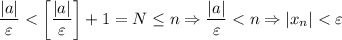
А значит, если взять $N=\left[\dfrac{|a|}{\varepsilon}\right] +1$ (*), $\forall\;n\geq N\to |x_n|$ . И правда: $\dfrac{|a|}{\varepsilon}$

(*) Очевидно, что для любого допустимого значения $\varepsilon$ выражение $\left[\dfrac{|a|}{\varepsilon}\right] +1$ определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (*)

А это и означает, что предел данной последовательности равен 0

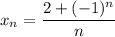
4) $x_n=\dfrac{2+(-1)^n}{n}$

|x_n|

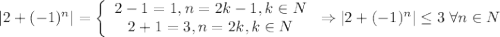
$|2+(-1)^n|=\left\{\begin{array}{c}2-1=1,n=2k-1,k\in N \\2+1=3,n=2k,k\in N \end{array}\right. \Rightarrow |2+(-1)^n|\leq 3\; \forall n\in N$

А значит, если взять $N=\left[\dfrac{3}{\varepsilon}\right] +1$ (**), $\forall\;n\geq N\to |x_n|$ . И правда: $\dfrac{|2+(-1)^n|}{\varepsilon}\leq\dfrac{3}{\varepsilon}< \left[\dfrac{3}{\varepsilon}\right] +1=N\leq n \Rightarrow \dfrac{|2+(-1)^n|}{\varepsilon}< n \Rightarrow |x_n|$

(**) Очевидно, что для любого допустимого значения $\varepsilon$ выражение $\left[\dfrac{3}{\varepsilon}\right] +1$ определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (**)

А это и означает, что предел данной последовательности равен 0

___________________________

2) a=1. Тогда 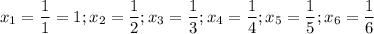$x_1=\dfrac{1}{1}=1; x_2=\dfrac{1}{2}; x_3=\dfrac{1}{3}; x_4=\dfrac{1}{4}; x_5=\dfrac{1}{5}; x_6=\dfrac{1}{6}$

$x_1=\dfrac{2+(-1)^1}{1}=1;\;x_2=\dfrac{2+(-1)^2}{2}=1\dfrac{1}{2};\;x_3=\dfrac{2+(-1)^3}{3}=\dfrac{1}{3};\;x_4=\dfrac{2+(-1)^4}{4}=\dfrac{3}{4};\;x_5=\dfrac{2+(-1)^5}{5}=\dfrac{1}{5};\;x_6=\dfrac{2+(-1)^6}{6}=\dfrac{1}{2}.$

___________________________

Обозначения и некоторые св-ва: {x} - дробная часть числа x, [x] - целая часть числа x. 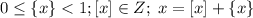$0\leq \{x\}$

пример 2 и 4. Все теоремы и аксиомы, будьте добры, распишите. Действий, пусть и банальных, легких не

4,6(34 оценок)

Ответ:

nataliyapotehi

09.04.2020

В задаче, очевидно, некорректное условие.

Если действительно надо найти площадь треугольника АВС, то это обыкновенная планиметрическая задача:

Из прямоугольного треугольника АВС по теореме Пифагора:

ВС = √(АВ² - АС²) = √(25² - 24²) = √((25 - 24)(25 + 24)) = √49 = 7

Площадь прямоугольного треугольника равна половине произведения катетов:

Sabc = 1/2 · AC · BC = 1/2 · 24 · 7 = 84 кв. ед.

Если же надо найти площадь другого треугольника, то в задаче не хватает данных, чтобы "выйти" из плоскости треугольника АВС (нужна длина хотя бы одного из данных перпендикуляров или угол между плоскостью α и плоскостью треугольника)

4,6(25 оценок)

Это интересно:

Компьютеры-и-электроника

09.08.2022

Как открыть IMG-файл на компьютере: подробное руководство...

Праздники-и-традиции

04.06.2020

Как отпраздновать Новый Год с ограниченной суммой денег...

Питомцы-и-животные

26.06.2022

5 простых шагов: как разводить гуппи в домашних условиях...

Питомцы-и-животные