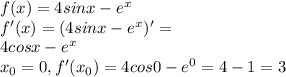
Здесь есть несколько простых правил. Смотри:
1) 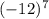 и
и 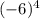
Есть правило о том, что любое число в чётной степени всегда 
То есть если мы (-6) возводим в чётную степень 4, то знак меняется с "минуса" на "плюс".
А вот с нечётной степенью это не работает. То есть если мы возводим (-12) в нечётную степень 7, то знак остаётся такой, какой был. А мы знаем, что любое отрицательное число всегда меньше положительного. Поэтому 
2) 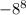 и
и 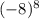
Здесь ещё проще. Под числом -8 мы понимаем -1*8. В первом случае (где без скобок записано) в восьмую степень возводится только сама 8, а "минус единица", можно сказать, остаётся за скобкой. Примитивно можем записать так:

Поэтому когда возводим 8 в восьмую (чётную) степень, знак всё равно не меняется, так как - 1 у нас осталось с таким же знаком "минус".
А вот во втором случае (где скобки) скобками нам показывают, что в чётную степень 8 возводиться как - 1, так и сама 8. Поэтому как ни крути, получим положительное число:

Значит, 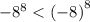
На первую формулу:
(a+b)²=a²+2ab+b²
(7+3)²=7²+2*7*3+3²=49+42+9=100
(40+1)²=40²+2*40*1+1²=1600+80+1=1681
На вторую формулу:
(a-b)²=a²-2ab+b²
(15-13)²=15²-2*15*13+13²=225-390+169=4
(100–2)²=100²-2*100*2+2²=10000–400+4=9604
На третью формулу:
(a+b)(a-b)=a²-b²
(12+1)(12-1)=12²-1²=143
(5+3)(5-3)=5²-3²=16
На четвёртую формулу:
(a+b)³=(a³+3a²b+3ab²+b³)
(3+2)³=3³+3*3²*2+3*3*2²+2³=27+54+36+8=125
На пятую формулу:
(a-b)³=(a³-3a²b+3ab²-b³)
(7-6)³=7³-3*7²*6+3*7*6²-6³=343-882++756-216=1
На шестую формулу:
a³+b³=(a+b)(a²-ab+b²)
3³+6³=(3+6)(3²-3*6+6²)=9*27=243
На седьмую формулу:
a³-b³=(a-b)(a²+ab+b²)
5³-2³=(5-2)(5²+5*2+2²)=3*39=117
В итоге получилось 7 формул сокращённого умножения и 10 примеров.