Если я все правильно понял, то в основании лежит квадрат. радиус вписаной окружности будет равен половине стороны основания( 6/2= 3). высота боковой грани это гепотинуза и получается, что высота в квадрате = 4 в квадрате + 3 в квадрате = 25 и получается что высота равна корень из 25 т.е = 5см
2)пусть x- вычитаемое, и так как оно состтовляет 100 % то уменьшаемое равно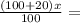 
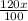. Теперь отнимем от
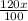, x получим что разность равно 
Составим пропроцию 1,2x --- 100%
0,2x ---y
Получим что y=50/3
ответ : 50/3 процентов это примерно 17 процентов
3) Увеличить число на 200% значит умножить его на 3, а уменьшить на 50 % значит умножить число на 0,5. пусть числитель дроби равен x а знаменатель равен y. После изменений получим дробь: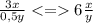 
Это значит что дробь увеличиться в 6 раз
Если ещё не изучено понятие производной, то решение может быть таким:
1. -2;
2. 3.
Объяснение:
1.Sn=6n-n^2
a1 = S1 = 6•1 - 1^2 = 5;
a1+a2 = S2 = 6•2 - 2^2 = 12 - 4 = 8;
a2 = S2 - S1 = 8 - 5 = 3.
Найдём d:
d = a2 - a3 = 3 - 5 = -2.
2. Sn=6n-n^2
Рассмотрим квадратичную функцию
у = 6х - х^2.
Графиком функции является парабола
у = - х^2 + 6х
Ветви параболы направлены вниз, своего наибольшего значения функция достигает в вершине параболы. Найдём её координаты:
х вершины = -b/(2a) = -6/(-2) = 3.
y вершины = - 3^2 +6•3 = -9+18 = 9.
Наибольшего значения 9 функция у = - х^2 + 6х достигает при х = 3.
Так как 3 - натуральное число, то и наша функция Sn=6n-n^2, определённая только для натуральных n, достигает наибольшего значения 9 при n = 3.
Необходимо взять три первых члена прогрессии, чтобы их сумма была наибольшей и равной 9.
ответить на второй вопрос можно и по-прежнему другому:
Sn=6n-n^2
- n^2 + 6n = - (n^2 - 6n) = - (n^2 -2•n•3 + 9 - 9) = - ((n-3)^2 -9) = - (n-3)^2 + 9.
Так как слагаемое 9 постоянно, a - (n-3)^2 неположительно для любого n, то наибольшей сумма будет тогда, когда наибольшим будет первое слагаемое, т.е. когда - (n-3)^2 = 0, при n = 3.
В этом случае Sn = - (n-3)^2 + 9 = 0 + 9 = 9.
Обозначения можете свои ввести,простите за рисунок программа не позволяет делать прозрачные линии