Объяснение:
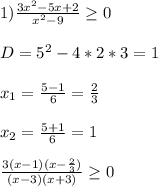
+ - + - +
_____-3_________2/3______1___________3_______
x∈(-∞;3)∪[2/3; 1]∪(3; +∞)
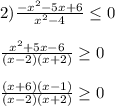
+ - + - +
_______-6____________-2______1______2______
x∈(-∞; -6]∪(-2; 1]∪(2; +∞)
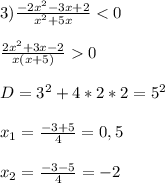
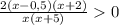
+ - + - +
_____-5__________-2_____0____0,5______
x∈(-∞; -5)∪(-2; 0)∪(0,5; +∞)
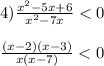
+ - + - +
_______0_______2______3_________7________
x∈(0;2)∪(3;7)
если 8х-15х^2-1 - это подкоренное выражение, то оно должно быть больше или равно 0.
решаем: -15х^2+8х-1 больше либо равно 0
15х^2-8х+1 меньше либо равно 0 (умножили на -1!)
15х^2-8х+1=0 и находим дискриминант: Д=64-4*15*1=4, значит еорень из Д=2, находим корни х1=(8-2)/2*15=0,2 ; х2=(8+2)/2*15=1/3.
(х-0,2)(х-1/3) меньше либо равно 0.
с промежутков находим: х принадлеж.[0,2;1/3]
значит х может быть равным от 0,2 до 1/3. Область определения функции или ОДЗ - это значения, которые принимает х, и чтобы выражение или неравенство имело смысл
13) непонятная запись, возможно
81*3/4=60.75
18) (0,5+0,2i)-(-0,2+0,5i)=0.5+0.2i+0.2-0.5i=0.7-0.3i
20) f(x)=-x^4+8x^2, a=-2
f'(x)=-4x^3+16x
f(a)=-(-2)^4+8(-2)^2=-16+32=16
f'(a)=-4(-2)^3-16*2=32-32=0
y=f(a)+f'(a)(x-a)=16
y=16 - уравнение касательной
22) y=-x^2+2x, y=x^2-2x
находим точки пересения графиков
-x^2+2x=x^2-2x
-2x^2+4x=0
-2x(x-2)=0
x=0, x=2
берем интеграл
int ((-x^2+2x)-(x^2-2x))dx; x=0..2=8/3 - искомая площадь