Распишем цифры разрядов x, y, 4 искомого десятичного числа как:
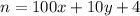
"Зачеркнём последнюю цифру", получив двузначное число:
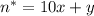
Соотношение между ними ("число уменьшится на 274"):
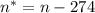
Преобразуем:
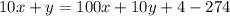
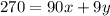
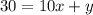
Цифра первого разряда (y) как функция цифры второго разряда (x):
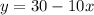
У этого уравнения бесконечное множество решений. Однако, поскольку это цифра, то имеем ограничения:
x, y - натуральные числа или 0 (цифры),
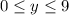 ,
,
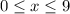 .
.
То есть:
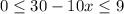
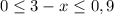
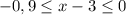
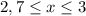
Единственным решением для целых x в заданном промежутке будет число (цифра!) 3.
Тогда y будет: y = 30 - 10*3 = 0.
Итак, ответ:
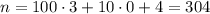
Нужно использовать следующие свойства числовых неравенств:
1. К обеим частям верного числового неравенства можно прибавить одно и то же число и получится верное числовое неравенство, т.е.:
если а < b и с - любое число, то a + c < b + c.
2. Обе части верного числового неравенства можно умножить (разделить) на одно и то же положительное число, при этом получиться верное числовое неравенство; если же число отрицательное, то знак неравенства изменится на противоположный, т.е.:
если а < b и с > 0, то ac < bc;
если а < b и с < 0, то ac >bc.
Таким образом, если а < b, то: 2,5а < 2,5b (2,5 > 0),
а затем и 2,5а - 7 < 2,5b - 7.
ответ: 2,5а - 7 < 2,5b - 7.