Question

Задан треугольник с координатами вершин а (-2, 4), в (6; -2), с (8, 7). методом аналитической найти: длину ав, уравнение сторон ав и вс те их угловые коофициеенты, уравнения медиан проведенных из вершин а и в, вершину а, уравнения и высоту вершины с, площадь треугольника; уравнение прямой, проходящей через точку с параллельна ав.

Answer 1

1) $AB=\sqrt{(6+2)^2+(-2-4)^2}=10$

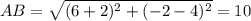
2) Составим уравнение АB:

$\frac{x+2}{6+2}=\frac{y-4}{-2-4} \\\ \frac{x+2}{8}=\frac{y-4}{-6} \\\ \frac{x+2}{4}=\frac{y-4}{-3} \\\ 3x+6=16-4y \\\ 3x+4y-10=0$

Это требуемое уравнение. Коэффициент АВ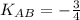 $K_{AB}=-\frac{3}{4}$

3) Составим уравнение ВС: 

$\frac{x+2}{10}=\frac{y-4}{3} \\\ 3x+6=10y-40 \\\ 3x-10y+46=0$

Это требуемое уравнение. Коэффициент BC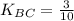 $K_{BC}=\frac{3}{10}$

4) Пусть АМ-медиана. M- середина ВC

$M=(\frac{6+8}{2}; \ \frac{-2+7}{2})=(7; 2.5)$

Составим уравнение AM: 

$\frac{x+2}{7+2}=\frac{y-4}{2.5-4} \\\ x+2=-6y+24 \\\ x+6y-22=0$

Это требуемое уравнение.

5) Пусть BN-медиана. N- середина AC

$N=(\frac{-2+8}{2}; \ \frac{4+7}{2})=(3; 5.5)$

Составим уравнение BN: 

$\frac{x-6}{3-6}=\frac{y+2}{5.5+2} \\\ 15-2.5x=y+2 \\\ 5x+2y-26=0$

Это требуемое уравнение.

6) Пусть СК-высота к стороне АВ.

Тогда СК и АВ взаимно перпендикулярны, причем 

$K_{CK}*K_{AB}=-1, \\\ K_{CK}=\frac{-1}{K_{AB}}=\frac{4}{3} \\\ y=K_{CK}x+b \\\ y=\frac{4}{3}x+b \\\ A(-2; 4) \in y, \ \frac{4}{3}*(-2)+b=4 \\\ b=\frac{20}{3} \\\ y=\frac{4}{3}x+\frac{20}{3} \\\ 4x-3y+20=0$

Это уравнение высоты СК.

7) Площадь треугольника АВС 

$S_{ABC}=б\frac{1}{2}*|AB \times AC|=б\frac{1}{2}*\left[\begin{array}{ccc}-2-8&4-7\\6-8&-2-7\end{array}\right]= \\\ =б\frac{1}{2}*\left[\begin{array}{ccc}-10&-3\\-2&-9\end{array}\right]=\frac{1}{2}*(90-6)=42$

8) Пусть CF||AB, тогда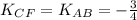 $K_{CF}=K_{AB}=-\frac{3}{4}$ 

$y=K_{CF}x+b \\\ y=-\frac{3}{4}x+b \\\ C(8; 7) \in y, \ -\frac{3}{4}*8+b=7 \\\ b=13 \\\ y=-\frac{3}{4}x+13 \\\ 3x+4y-52=0$/

Это уравнение прямой CF||AB.