Пусть  - канонический базис в
- канонический базис в 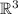 .
.
Тогда матрицу перехода 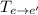 можно найти следующим образом:
можно найти следующим образом:
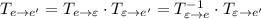
Если записать блочную матрицу 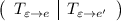 и привести путем элементарных преобразований к виду
и привести путем элементарных преобразований к виду  , то
, то 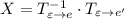
Матрицу 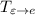 легко получить: достаточно записать в столбцы координаты векторов базиса
легко получить: достаточно записать в столбцы координаты векторов базиса  . Аналогично с матрицей
. Аналогично с матрицей 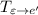 .
.
В итоге необходимо получить вид  следующей матрицы:
следующей матрицы:
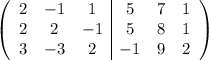
Вычтем первую строку из второй и третьей:
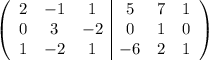
Вычтем из первой строки 2 третьих и поменяем их местами:
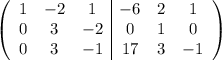
Вычтем из третьей строки вторую:
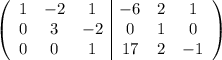
Прибавим ко второй строке 2 третьих и вычтем из первой третью:

Делим вторую строку на 3:
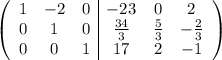
Прибавляем в первой строке 2 вторых:
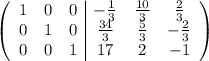
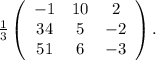
15км/ч
Объяснение:
я сокращу названия: дом=Д
автостанция=А
пусть скорость велосипедиста
от А до Д =х, тогда скорость
от Д до А=х+3. Зная, что расстояние от Д до А= 30км и разница во времени составила 30 минут, составим уравнение:
30минут=1/2часа
найдём общий знаменатель:
перемножим числитель и знаменатель соседних
дробей между собой крест накрест и получим:
х²+3х=90×2
х²+3х=180
х²+3х–180=0
Д=9–4(–180)=9+720=729
х1=(–3–27)/2= –30÷2= –15
х2=(–3+27)/2=24/2=12
х1 нам не подходит поскольку скорость не может быть отрицательной поэтому используем х2=12
Итак: скорость велосипедиста от А до Д=12км/ч, тогда скорость от дома до А=12+3=15 км/ч