5 чёрных шариков
Объяснение:
формула вероятности р = Ν пол. / Ν всех
Ν пол. - количество положительных исходов
Ν всех - количество всех исходов
Положительные исходы: чёрные шарики - Х шт
Не положительные исходы: жёлтые шарики - 15 шт
Все исходы: чёрные + жёлтые= Х+15 шт
Вероятность р = Ν пол. / Ν всех, то есть 1/4 = Х / Х+15
решим уравнение: 1/4 = Х / (Х+15)
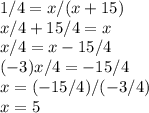- чёрных шариков.
ВТОРОЙ ВАРИАНТ РЕШЕНИЯ.
Можно решить проще, логическим решением.
ЧШ - чёрные шарики
ЖШ - жёлтые шарики
ВШ - все шарики вместе
Вероятность р = Ν пол. / Ν всех, то есть р = ЧШ / ВШ
Жёлтых ш. - 15; чёрных ш. - Х; всех ш. - 15+х
Если вероятность р = 1/4, это отношение чёрных к общему количеству: ЧШ / ВШ = 1/4. То тогда отношение ЖШ / ВШ = 3/4
И раз 3/4 - это 15 шариков (жёлтых), то соответственно 1/4 - это 5 шариков (чёрных)
Рассмотрим выражение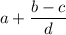 
. Чтобы оно было наименьшим, необходимо, чтобы выражения 
и 
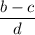были наименьшим.
Заметим, что выражение 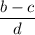может быть отрицательным. Если его числитель будет наименьшим отрицательным, а знаменатель - наименьшим положительным, то оно примет наименьшее значение. Значит, 
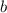необходимо выбрать наименьшим, 
- наибольшим,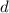 
- наименьшим.
Наибольшее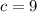 
. Наименьшие значения 2, 3, 4 нужно распределить между выражениям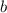и , и 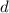. Проверим все варианты.
Пусть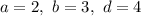 
. Тогда: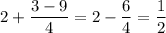 
Пусть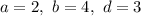 
. Тогда: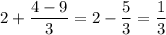 
Пусть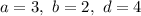 
. Тогда: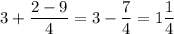 
Пусть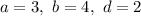 
. Тогда: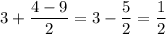 
Пусть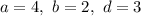 
. Тогда: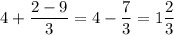 
Пусть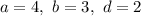 
. Тогда: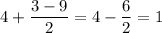 
Наименьшее значение равно 1/3.
ответ: 1/3
для того чтобы решить линейное неравенство нужно:
1)перенести иксы в одну часть а числа в другую
2)при умножении или делении на отрицательное число знак меняется
3)найти значения икса при которых левая часть принимает значение нуля
4)и отметить нужный промежуток
а для решения системы нужно решить оба неравенства и отметить пересечение неравенств