сos(2пи+5х)+sin(пи/2-х)=cos2x
cos 5x + cos x = cos 2x
2cos3x * cos 2x = cos 2x
2cos3x=1
cos3x=1/2
3x=+- arccos 1/2 + 2pk
3x= +- p/3 + 2pk
x = +- p/9 + 2pk/3
2cos3x * cos 2x = cos 2x
cos2x(2cos3x-1)=0
cos2x=0
2x=p/2 + pk
x = p/4 + pk/2
а) f(x) = x/5 + 1
x/5 + 1 < 0 ⇒ x/5 < -1 ⇒ x < -5
f(x) < 0 при х ∈ (-∞; -5)
f(x) = 0 при х = -5
f(x) > 0 при х ∈ (-5 ; +∞)
б)
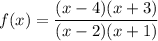
Решаем задачу методом интервалов
1) находим точки нулевых значений функции
х - 4 = 0 ⇒ х = 4
х + 3 = 0 ⇒ х = -3
2) находим точки разрыва функции
х - 2 = 0 ⇒ х = 2
х + 1 = 0 ⇒ х = - 1
Делим числовую прямую на интервалы и определяем знаки функции в этих интервалах
---( + )-------- -3 ---( - )-------- -1 ----( + )---------- 2 ----( - )---------- 4 ------(+) ----------
f(x) < 0 при х ∈ (-3; -1)∪(2; 4)
f(x) > 0 при х ∈ (-∞; -3)∪(-1; 2)∪(4; +∞)
формул приведения упростим и получим:
cos 5x + cos x = cos 2x
Далее
2cos 3x cos 2x - cos 2x = 0
cos 2x (2 cos 3x - 1)=0
cos 2x=0 или cos 3x = 1/2
Найдем наибольший отрицателльный корень: х = -П/9