48
Объяснение:
Для начала изобразим это число как определенное количество позиций:
_ _ _ _ _
На каждой позиции мы будем записывать сколько цифр на этой позиции может стоять. Потом, чтобы найти количество чисел, мы переумножим значения этих позиций.
Так как все цифры разные, на пятой позиции может стоять одна из пяти цифр, на четвёртой одна из четырёх оставшихся, на третей одна из трёх, на второй одна из двух, и одна на первой. То есть, значения позиций выглядели бы так:
1 2 3 4 5
Но, также известно, что числа должны быть парными, а значит на последней позиции может находится только одна из двух цифр:
1 2 3 4 2
Соответсвенно, переумножением отмеченных этих цифр мы получим количество вариантов:
1 × 2 × 3 × 4 × 2 = 48
Кусочно- заданная функция - это функция , которая на различных промежутках оси ОХ задаётся разными функциями. ( Как бы на разных "кусочках" оси ОХ задаются разные функции).
На промежутке (-∞ ; -2 ] функция представляет из себя гиперболу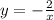 
. График гиперболы рисуем только на этом промежутке (сплошной линией), оставшаяся часть графика на промежутке (-2 ; +∞) стирается (либо рисуется пунктирной линией). Точка с абсциссой х= -2 , точка (-2,1) , принадлежит этому графику.
На промежутке (-2 ; 2] рисуем график у=|x|-1 . Это график функции у=|x|, который смещён на 1 единицу вниз по оси ОУ. Точка (-2,1) не принадлежит графику, а точка (2, 1) принадлежит графику.
На промежутке (2 ; + ∞) рисуем график функции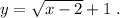 
Это график функции 
, смещённый вдоль оси ОХ на 2 единицы вправо и вдоль оси ОУ на 1 единицу вверх . Точка (2,1) не принадлежит графику функции.
График кусочно заданной функции нарисован сплошными линиями.
решение смотри на фотографии