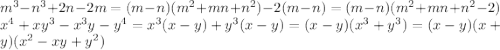

1) M^3 - N^3 + 2N - 2M = (M-N)*(M^2 +MN + N^2) + 2*(N - M) = (M-N)*(M^2+MN+N^2+2)
2) X^4 +XY^3 -X^3*Y - Y^4 = (X^4 - X^3Y) + (XY^3 - Y^4) = X^3*(X - 1) + Y^3*(X - 1) =
= (X-1)*(X^3 + Y^3)
3) 5X*(X-3)^2 - 5*(X-1)^3 + 15*(X+2)*(X-2) = 5
5X*(X^2-6X+9)- 5*(X-1)*(X^2+ X + 1) +15*(X^2 - 4) = 5
5X^3 - 30X^2 + 45X -5X^3 + 5 + 15X^2 - 60 = 5
15X^2 + 45X - 60 = 0
15*(X^2 + 3X - 4)= 0
D = 9-4*1*(-4) = 25
V D = 5
X1 = (- 3 + 5 )\ 2 = + 1
X2 = - 8 \ 2 = - 4
ОТВЕТ: 1 и минус 4

1. Преобразуем уравнение:
4х^2 + 12х + 12/х + 4/х^2 = 47;
4(х^2 + 2 + 1/x^2) - 8 + 12(х + 1/х) - 47 = 0;
4(х + 1/x)^2 + 12(х + 1/х) - 55 = 0.
2. Замена:
х + 1/x = t;
4t^2 + 12t - 55 = 0;
D/4 = 6^2 + 4 * 55 = 36 + 220 = 256 = 16^2;
t = (-6 ± 16)/4;
t1 = (-6 - 16)/4 = -22/4 = -11/2;
t2 = (-6 + 16)/4 = 10/4 = 5/2.
3. Обратная замена:
х + 1/x = t;
х^2 + 1 = tx;
х^2 - tx + 1 = 0;
1) t = -11/2;
х^2 + 11/2 * x + 1 = 0;
2х^2 + 11x + 2 = 0;
D = 11^2 - 4 * 2 * 2 = 121 - 16 = 105;
x1/2 = (-11 ± √105)/4;
2) t = 5/2;
х^2 - 5/2 * x + 1 = 0;
2х^2 - 5x + 2 = 0;
D = 5^2 - 4 * 2 * 2 = 25 - 16 = 9;
x = (5 ± √9)/4 = (5 ± 3)/4;
x3 = (5 - 3)/4 = 2/4 = 1/2;
x4 = (5 + 3)/4 = 8/4 = 2.
ответ: (-11 ± √105)/4; 1/2; 2.