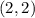
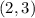
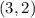
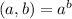- где a-число оценок, b-число учеников.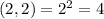
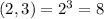
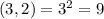
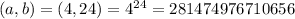
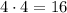- варианта событий.
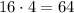- варианта событий.
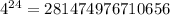- вариантов событий.
1. -2;
2. 3.
Объяснение:
1.Sn=6n-n^2
a1 = S1 = 6•1 - 1^2 = 5;
a1+a2 = S2 = 6•2 - 2^2 = 12 - 4 = 8;
a2 = S2 - S1 = 8 - 5 = 3.
Найдём d:
d = a2 - a3 = 3 - 5 = -2.
2. Sn=6n-n^2
Рассмотрим квадратичную функцию
у = 6х - х^2.
Графиком функции является парабола
у = - х^2 + 6х
Ветви параболы направлены вниз, своего наибольшего значения функция достигает в вершине параболы. Найдём её координаты:
х вершины = -b/(2a) = -6/(-2) = 3.
y вершины = - 3^2 +6•3 = -9+18 = 9.
Наибольшего значения 9 функция у = - х^2 + 6х достигает при х = 3.
Так как 3 - натуральное число, то и наша функция Sn=6n-n^2, определённая только для натуральных n, достигает наибольшего значения 9 при n = 3.
Необходимо взять три первых члена прогрессии, чтобы их сумма была наибольшей и равной 9.
ответить на второй вопрос можно и по-прежнему другому:
Sn=6n-n^2
- n^2 + 6n = - (n^2 - 6n) = - (n^2 -2•n•3 + 9 - 9) = - ((n-3)^2 -9) = - (n-3)^2 + 9.
Так как слагаемое 9 постоянно, a - (n-3)^2 неположительно для любого n, то наибольшей сумма будет тогда, когда наибольшим будет первое слагаемое, т.е. когда - (n-3)^2 = 0, при n = 3.
В этом случае Sn = - (n-3)^2 + 9 = 0 + 9 = 9.
Пусть х производительность первого рабочего, а у-второго рабочего
Поскольку после 3 часов работы первого рабочего был сделан объем работ 3х, второй сделал
(3-1)*у =2у.
Всего было сделано 1-0,45 =0,55 объема работ
Или запишем первое уравнение
3x+2y =0,55
Выразим из уравнения y
y = (0,55-3x)/2
По окончанию работы кажды сделал ровно половину объема работ
Время потраченное первым рабочим составило
1/(2x)
Время потраченное вторым рабочим составило
1/(2y)
Так как второй потратил на 1 час меньше запишем второе уравнение
1/(2x) - 1/(2y) =1
Поскольку х и у одновременно не равняются нулю то умножим обе части уравнения на 4х*у
2у-2х=4ху
Подставим выражение для у полученное выше у=(0,55-3х)/2
0,55-3x-2x =2x(0,55-3x)
0,55-5x =1,1x-6x^2
6x^2-6,1x+0,55 =0
D =6,1^2-4*6*0,55 = 24,01
x1=(6,1-4,9)/12 = 0,1
x2=(6,1+4,9)/12=11/12
Найдем у
y1 =(0,55-3*0,1)/2=0,25/2=0,125
y2=(0,55-3*(11/12))/2=(0,55-11/4)/2 =-1,1 ( Производительность не может быть отрицательной)
Поэтому х2=11/12 также не удолетворяет решению
Найдем время потраченное каждым рабочим на выполнение работы
t1 =1/x1=1/0,1 =10 часов
t2=1/y1 =1/0,125 =8 часов