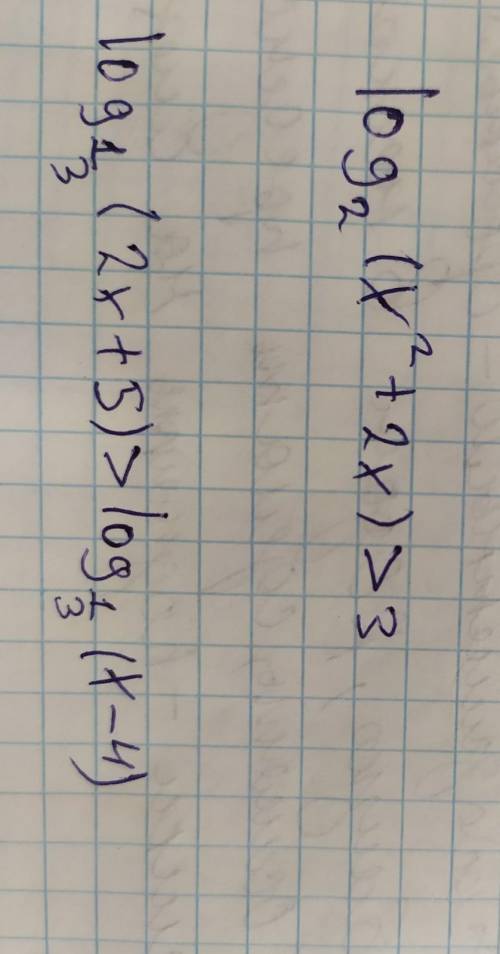
Количество все возможных событий: 6"6-36 Выпишем все варианты выпавших очков, в сумме которых дадут 8 (2;6], (3;5), (4;4), [5%;3], (6;2] - 5 вариантов (число благоприятных событий) Вероятность того, что сумма выпавших очков равна 8 Р(A) %3D 5/36 Событие В — "произведение выпавших очков равно 8" Таких вариантов можно привести подбором: (2;4), (4;2)- всего 2 варианта (число благоприятных событий) Искомая вероятность: Р(В) %3 2/36 %3D 1/18 Событие С — сумма выпавших очков больше, чем произведение (136], [1;5), (1;4), (1;3}, (1;2}, (1;1) - всего 6 и с учетом симметричности всего будет 5+6%11 вариантов Искомая вероятность: Р(C) - 11/36.
В решении.
Объяснение:
Катер пройшов за течією річки за 2 години таку саму відстань як і за 2 години 15 хвилин проти течії річки. Яка власна V катера якщо V течії - 3 км/год.
Катер по течению реки за 2 часа такое же расстояние как и за 2 часа 15 минут против течения реки. Какая собственная скорость катера, если скорость течения реки - 3 км/час.
Формула движения: S=v*t
S - расстояние v - скорость t – время
х - собственная скорость катера.
х + 3 - скорость катера по течению.
х - 3 - скорость катера против течения.
2 часа 15 минут = 2,25 часа.
Расстояние по течению и против одно и то же.
По условию задачи уравнение:
(х + 3) * 2 = (х - 3) * 2,25
2х + 6 = 2,25х - 6,75
2х - 2,25х = -6,75 - 6
-0,25х = -12,75
х = -12,75/-0,25
х = 51 (км/час) - собственная скорость катера.
Проверка:
54 * 2 = 108 (км);
48 * 2,25 = 108 (км);
108 = 108, верно.
а) x€ (-∞;-4)U(2;+∞)
б) x€∅
Объяснение:
N°1:
Т. к. основание логарифма 2 > основание 1 => знак неравенства не меняется
D = b²-4ac = 4+32 = 36 = 6²
х1= 2; х2 = -4
(х-2)(х+4) > 0
х€ (-∞; -4)U(2;+∞)
ОДЗ: х²+2х > 0
х(х+2) > 0
Значит:
х€ (-∞; -2)U(0;+∞)
Получаем систему:
{x€ (-∞;-4)U(2;+∞)
{x € (-∞;-2)U(0;+∞)
Отсюда:
x€ (-∞;-4)U(2;+∞)
ответ: x€ (-∞;-4)U(2;+∞)
N°2:
Т. к основание логарифма 1/3 < основания 1 => знак неравенства меняется
2х+5 < х-4
х <-9
Значит:
х€ (-∞; -9)
ОДЗ:
{2х+5 > 0
{х-4 > 0
Получаем:
{х> -2,5
{х>4
Значит:
х€ (4;+∞)
Получаем систему:
{х€ (-∞;-9)
{х€ (4;+∞)
Отсюда: х€∅
ответ: х€∅