опытаемся найти точки их пересечения, решив систему:
(x-2) 2 + (y-3) 2=16
(x-2) 2 + (y-2) 2=4
(x-2) 2=16 - (y-3) 2
(x-2) 2=4 - (y-2) 2,
отсюда 16 - (y-3) 2=4 - (y-2) 2
16-у2+6 у-9=4-у2+4 у-4 ещё
6 у-4 у=4-4+9-16 ещё
2 у=-7 найдём игрек
у=-3,5 и попробуем найти икс
(x-2) 2=4 - (-3,5-2) 2
(x-2) 2=4-30,25
(x-2) 2=-25,75, а квадрат не может быть отрицательным, следовательно, эти две окружности не пересекаются. центры окружностей - в точках (2; 3) и (2; 2) соответственно, то есть расстояние между центрами равно единице, а радиусы - 4 и 2, то есть вторая, меньшая, окружность расположена внутри первой.
ответ: малая окружность расположена внутри большой.
Пусть начальная цена 1 стола была х рублей, а начальная цена 1 стула была у рублей. Тогда за два стола и шесть стульев надо заплатить 2*х+6*у рублей, что по условию задачи 232 рубля.
Получаем первое уравнение: 2*х+6*у = 232
После того, как столы подешевели на 15%, они стали стоить (х-0,15х) рублей (т.к. 15% от х - это 0,15х, а когда они подешевели, от начальной цены отняли величину их удешевления).
После того, как стулья подешевели на 20%, они стали стоить (у-0,2у) рублей (т.к. 20% от у - это 0,2у, а когда они подешевели, от начальной цены отняли величину их удешевления)
Тогда за один стол и два стула по новым ценам заплатили 1*(х-0,15х) + 2*(у-0,2у) рублей, что по условию задачи 87,2.
Получаем второе уравнение: 0,85х+2*0,8у=87,2.
Решаем получившуюся систему:
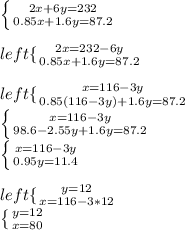
80 рублей - начальная цена стола, 12 рублей - начальная цена стула.
a3 = 4 1/3
n = 589
Объяснение:
a1 + a2 = a1 + (a1 + d) = 2a1 + d = 9 2/3 = 29/3
a1 - d = 5 1/3 = 16/3
Сложим эти 2 равенства:
3a1 + d - d = 3a1 = 29/3 + 16/3 = 45/3 = 15
a1 = 15/3 = 5
a1 - d = 16/3
d = a1 - 16/3 = 5 - 16/3 = 15/3 - 16/3 = -1/3
a3 = a1 + 2d = 5 - 2/3 = 4 1/3
aₙ = -191
a1 + (n-1)*d = -191
n-1 = (191 - a1)/d = (-191 - 5) / (-1/3) = (-196) / (-1/3) = 196*3 = 588
n = 588 +1 = 589