а) 4x² - 4x - 15 < 0
D = b² - 4ac = 16 + 4*4*15 = 16 + 240 = 256
x₁ = (-b + √D) / 2a = (4 + 16) / 8 = 20 / 8 = 2,5
x₂ = (-b - √D) / 2a = (4 - 16) / 8 = -12 / 8 = -1,5
(x - 2,5)(х + 1,5) < 0
{ x < 2,5
{ x < -1,5
ответ: (-1,5; 2,5)
б) x² - 81 > 0
(x - 9)(x + 9) > 0
{ x > -9
{ x > 9
ответ: (-9; 9)
в) x² < 1,7х
x² - 1,7х < 0
х(x - 1,7) < 0
{ x < 0
{ x < 1,7
ответ: (0; 1,7)
г) x( x + 3) - 6 < 3 (x + 1)
x² + 3x - 6 - 3x - 3 < 0
x² - 9 < 0
(x - 3)(x + 3) < 0
{ x < -3
{ x < 3
ответ: (-3; 3)
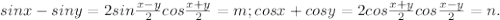
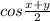. Выразим его из обоих равенств:
.
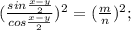
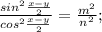
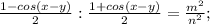
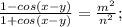
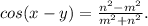
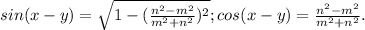
Объяснение:
(3x-4)² или 3x-4² - ... ?
Решаем для случая: (3x-4)²
(3x-4)²-(3x+7)(3x-7)+25x = 9х² -24х +16 -(9х² -49) +25х =
= 9х² + х + 16 - 9х² + 49 = х + 65
при х =5: х + 65 = 70