Объяснение:
1) при x≥0 IxI=x
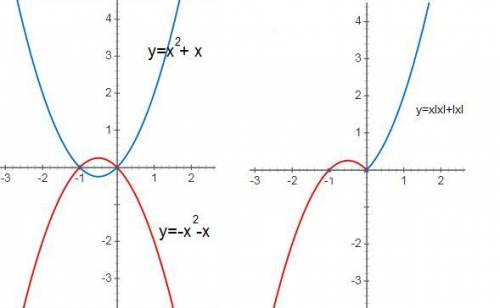
y=x²+x это парабола вершина в точке х=-b/2a=-1/2
y(-1/2)=0,25-0,5=-0,25
точки пересечения с осью ОХ x²+x=0 х(х+1)=0 х={-1;0}
строим график по эти точкам и оставляем только ту его часть где x≥0
2) при x<0 IxI=-x
y=-x²-x это парабола вершина в точке х=-b/2a=-1/2
y(-1/2)=-0,25+0,5=0,25
точки пересечения с осью ОХ -x²-x=0 -х(х+1)=0 х={-1;0}
строим график по эти точкам и оставляем только ту его часть где x<0
3) в задаче видимо имеется ввиду прямая у=m если так то
прямая у=m имеет с графиком одну общую точку при
m ∈(-∞;0)∪(0,25;+∞)
a)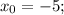
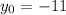
б)
ось симметрии параболы.
в)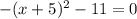
Левая часть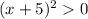
всегда положительна, поэтому 
∈{∅} , это означает, что данная функция не имеет точек пересечения с осью Ох;
г)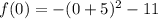
д) Ветви данной функции направлены вниз.