Лодка против течения 84 км и вернулась обратно. На обратный путь она затратила на 8 ч меньше. Собственная скорость лодки 10 км\ч. Найти скорость течения.
Решение: Пусть x-скорость течения, тогда первую часть пути она со скоростью (10-x) км\ч, а вторую (10+х) км\ч, время на первую часть пути , на вторую . Получаем уравнение:
Я уже решал эту задачу. Они выехали в момент 14-t, то есть за t ч до 14, и встретились в 14. Скорость велосипеда была v, скорость мотоцикла w км/ч. При движении навстречу скорости складываются. Расстояние AB=S. Значит, время в пути S = t*(v+w) Если бы скорость вела была 2v, то они встретились бы в 13 ч 30 мин, то есть на 0,5 ч раньше. S = (t-0,5)(2v+w) Если бы скорость мото была 2w, то они встретились бы в 13 ч 12 мин, то есть на 48 мин=0,8 ч раньше S = (t-0,8)(2w+v) Получаем систему { S = tv + tw { S = 2tv + tw - v - 0,5w { S = 2tw + tv - 1,6w - 0,8v Из 2 ур-ния вычитаем 1 ур-ние. Из 3 ур-ния тоже вычитаем 1 ур-ние. { 0 = tv - v - 0,5w { 0 = tw - 1,6w - 0,8v Решаем { w = 2v*(t-1) { 0,8v = w(t-1,6) = 2v(t-1)(t-1,6) Делим всё на 2v и умножаем на 5 2 = 5(t^2-2,6t+1,6) 5t^2 - 13t + 6 = 0 D = 13^2 - 4*5*6 = 169 - 120 = 49 t1 = (13-7)/10 = 6/10 = 0,6 ч = 36 мин. t2 = (13+7)/10 = 20/10 = 2 ч. Если t1, то они выехали в 14 ч - 36 мин = 13 ч 24 мин. Но это позже, чем 13 ч 12 мин, поэтому не подходит. ответ: они выехали в 14 - 2 = 12 часов.
Исходное число должно быть четырехзначным. Пусть исходное число будет ABCD=1000A+100B+10C+D. Из четырехзначного числа ABCD вычли сумму его цифр и получили 2016: 1000A+100B+10C+D-(А+В+С+D)=2016 Раскроим скобки и решим: 1000A+100B+10C+D-А-В-С-D=2016 999А+99В+9С=2016 Сократим на 9: 111А+11В+С=224 Очевидно, что 1<А>3, т.е. А=2 (2000). 111*2+11В+С=224 222+11В+С=224 11В+С=224-222 11В+С=2 С=2-11В, где С и В – натуральные положительные числа от 0 до 9. При значениях В от 1 до 9, С – отрицательное число. Значит В=0, тогда С=2-11*0=2 Получаем число 202D, где D - натуральное положительное число от 0 до 9, т.е. возможные исходные значения от 2020 до 2029. 9 – максимальное значение D, значит наибольшее возможное исходное значение 2029. Проверим: 2029 – (2+2+0+9)=2029-13=2016 ответ: наибольшее возможное исходное значение число 2029
Лодка против течения 84 км и вернулась обратно. На обратный путь она затратила на 8 ч меньше. Собственная скорость лодки 10 км\ч. Найти скорость течения.
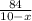 ,
,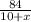 . Получаем уравнение:
. Получаем уравнение:
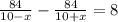
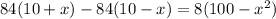
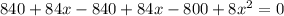
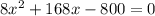
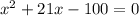
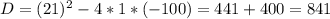
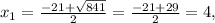 удоволетворяет условию задачи.
удоволетворяет условию задачи.
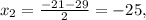 не удоволетворяет условию задачи.
не удоволетворяет условию задачи.
Решение:
Пусть x-скорость течения, тогда первую часть пути она со скоростью (10-x) км\ч, а вторую (10+х) км\ч, время на первую часть пути
на вторую
ответ: скорость течения равна 4 км\ч.